
Согласно теореме Безу остаток от деления полинома на двучлен равен значению полинома в корне этого двучлена,в данной задаче на полином G(x) никаких дополнительных условий не наложено,значит он может быть неприводимым над полем вещественных чисел,однако все равно раскладываться в произведение двучленов вида 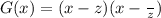
Где 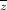 комплексно сопряжен z.
комплексно сопряжен z.
Полином G(x) примет вид 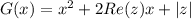
Re(z)-вещественная часть z,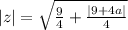 -модуль числа z.
-модуль числа z.
Очевидно,что подставляя получившиеся корни в исходный многочлен используя теорему Безу вычисление получается мягко говоря неудобным.
Аналогичная ситуация со схемой Горнера.
А вот при делении полиномов столбиком исходный многочлен представим в виде:
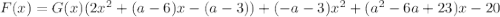
Очевидно,что степень остатка должна быть меньше степени делителя и мы можем остаток разделить на полином G(x),домноженный на (-a-3),тогда для того чтобы остаток от деления был равен нулю,то есть чтобы F(x) делился на G(x) должна выполняться система:
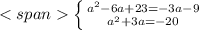
Которая не имеет решений ни в поле действительных,ни в поле комплексных чисел.
Значит ни при каких значениях a полином G(x) не является делителем F(x).
Понятно, что это квадратное уравнение. А когда квадратное уравнение будет иметь 2 различных отрицательных корня? Правильно, когда 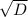 >-b, в данном случае b-коэффициент перед x.
>-b, в данном случае b-коэффициент перед x.
Приступаем к решениею, приведем уравнение к приведенному(разделим на 2)
x^2+1,5x+0,5a=0
Найдём дискриминант
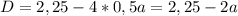
Т.к. в нашем уравнени b-отрицательное число (-1,5), то корню из дискриминанта достаточно принимать значения на промежутке
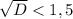
Потому что, если корень из дискриминанта будет больше 1,5 , то корни получатся либо положительными, либо равными нулю, а этого нам не надо.
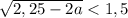
Возведем обе части в квадрат, чтобы избавиться от корня
2,25-2a<2,25
-2a<0
a>0
Значит, мы получим 2 различных отрицательных корня, если a>0.