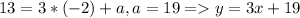. Кароче отсекаемый отрезок - это отрезок между 2-мя прямыми, как я его нашел, взял и угловой коэффициент сделал, как 1 получилось два уравнение у которых вместо 3х, просто х и между ними отрезок был бы равен 26 (= 19 + 7), но у нас не 1, а 3 угловой коэф. следовательно делим на 3 отрезок и получаем 8.(8), или 26/3 вот ответ.
=3(x+√5 )/(x+√5 )=3
x+√5
2) 7y-7√6
=7(y-√6 )/( y^2 + √5 )
y^2 + √5
3) t^2-19
=( t^2-19)/t-√19 =t+√19
t-√19
4) √23-s
=(√23-s)/( s^2-23)=-(s-√23)/( s^2-23)=-1/(s+√23)
s^2-23
5) √a+a
=(√a+a )/( 5(1+√a))=(√a)(1+√a)/( 5(1+√a))=(√a)/5 5+5√a
6) √2b-√2c
если так [(√2)b-(√2)c ]/(b-c)=(√2)(b-c)/(b-c)=(√2)
b-c
а если так,
√(2b)-√(2c )
=(√(2b)-√(2c) )/(b-c)=(√2)(√b-√c)/[(√b-√c)(√b+√c)]=(√2)/(√b+√c)
b-c