Решением данной системы является пара чисел: 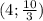 .
.
Объяснение:
Перед нами система уравнений с двумя неизвестными:
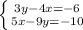
Данную систему уравнений проще решить, используя метод исключения одной переменной. Для этого домножим обе части первого уравнения на 3:
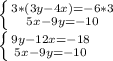
Теперь, сложим оба уравнения данной системы, чтобы избавиться от переменной y. Найдем x, путем упрощения обычного уравнения:
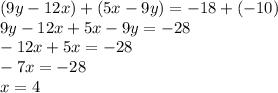
Теперь подставим данное значение в первое уравнение системы, чтобы найти y:
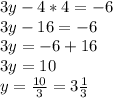
Получили ответ, что решением данной системы является пара чисел: 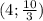
2*(x+y)²+3*(x+2*y)=5
-2*(x+y)+3*(x+2*y)=5
Полагая x+y=u, x+2*y=v, приходим к системе:
2*u²+3*v=5
-2*u+3*v=5
Вычитая из первого уравнения второе, получаем систему:
2*u²+2*u=0
-2*u+3*v=5
Из первого уравнения находим u1=0, u2=-1. Подставляя эти значения во второе уравнение, находим v1=(5+2*u1)/3=5/3, v2=(5+2*u2)/3=1. Возвращаясь к переменным x и y, получаем две системы:
x+y=0
x+2*y=5/3
и
x+y=-1
x+2*y=1
Решая первую систему, находим x1=-5/3, y1=5/3. Решая вторую систему, находим x2=-3, y2=2. ответ: -5/3,5/3 и -3,2.