ответ: x ∈ (-∞; 0) ∪ (3; +∞) .
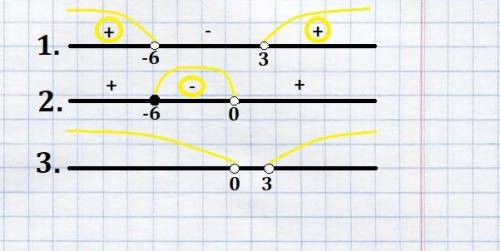
Сначала решим первое неравенство (методом интервалов). В первой скобке получается нуль, если подставить 3. Во второй - если подставить -6. Отмечаем эти числа на числовой оси и ставим нужные знаки (рисунок 1, в приложении). Знак неравенства строгий, поэтому все точки выколотые.
Теперь решаем второе неравенство. Нуль в числителе получается, если подставить -6 (точка закрашенная, знак неравенства нестрогий). А в знаменателе - если подставить 0 (точка выколотая, по всем правилам арифметики на нуль делить нельзя). Теперь ставим нужные знаки (рисунок 2, в приложении).
Теперь объединяем все решения двух неравенств (рисунок три, приложение) и записываем окончательный ответ:
x ∈ (-∞; 0) ∪ (3; +∞) .
Длина сада 175 м
Ширина сада 140 м
Объяснение:
х - длина сада
у - ширина сада
2,45 га = 24500 (м кв)
По условию задачи периметр сада 630 метров
Система уравнений:
2(х+у)=630
х*у=24500
Во втором уравнении выразим х через у и подставим выражение в первое уравнение:
х=24500/у
2(24500/у)+2у=630
49000/у+2у=630
Избавляемся от дробного выражения, умножаем все части уравнения на у:
49000+2у²=630у
2у²-630у+49000=0/2 делим на 2 для удобства вычислений:
у²-315у+24500=0, квадратное уравнение, ищем корни:
у₁,₂=(315±√99225-98000)/2
у₁,₂=(315±√1225)/2
у₁,₂=(315±35)/2
у₁=140 х₁=24500/140=175
у₂=175 у₂=24500/175=140
Так как по условию х - длина участка, а у - ширина,
решение системы уравнений х=175
у=140
Проверка:
175 * 140 = 24500 (м кв)= 2,45 га
2*(175+140)=630 (м) изгородь сада, периметр. Всё верно.
теперь решаем:
log₃(2x -1) = 4
2x - 1 = 81
2x = 82
x = 41 (в ОДЗ входит)
ответ:41
2)Хорды задают ΔАВС. В этом треугольнике известны стороны: 4√3; 8 и 4 ( расстояние между серединами - это средняя линия ΔАВС
Проверим т. Пифагора:
(4√3)² = 48
4²=16
8²= 64
48 +16 = 64
ответ: ΔАВС - прямоугольный.