Это просто
так как есть х²- это график параболы, при х² нет минуса, значит ветви параболы направлены вверх. Теперь надо найти точку пересечения параболы с осью ОУ .для этого х=0
у=0²-4*0-5=-5 . Точка пресечения с осью ОУ (0;-5)
Теперь найдём точки пересечения с осью ОХ (у=0)
х²-4х-5=0
D= 4²-4*1*(-5)=16+20=36

первая точка пересечения с осью ОХ (-1;0), вторая (5;0)
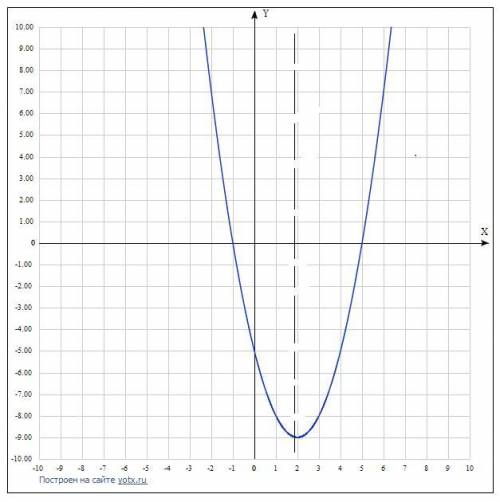
Посередине между этими точками будет ось симметрии параболы ( отметим штрихом на графике)
ну ещё пар точек определим при х=2
у= 2²-4*2-5= -9 точка(2;-9)- вершина параболы
Составим таблицу точек:
х | y
-2 | 7
-1 | 0
0 | 5
1 | -8
2 | -9
3 | -8
4 | -5
5 | 0
6 | 7
1.
а) 3(a + 2) + b(a + 2) = (3 + b) * (a + 2)
б) 4f(5m-3n) - 5r(5m-3n) = (4f - 5r) * (5m - 3n)
в) 5m(a - 3d) + a - 3d = 5m(a - 3d) + 1(a - 3d) = (5m + 1) * (a - 3d)
г) 5m(a - 3d) - a + 3d = 5m(a - 3d) + 1(a - 3d) = (5m + 1) * (a - 3d)
2.
а) 3a +6 + ab + 2b = 3(a + 2) + b(a + 2) = (3 + b) * (a + 2)
б) 20fr - 12fn - 25rm + 15mn = 4f(5r - 3n) - 5m(5r -3n) = (4f - 5m) * (5r - 3n)
в) ab + ac + af + b + c + f = a(b + c + f) + 1(b + c + f) = (a + 1) * (b + c + f) (думаю, у Вас тут ошибка, и должна быть именно буква b)
г) x⁵ + x⁴ + x³ +x² + x + 1 = x⁵ + x⁴ + x³ +x² + x¹ + 1 = x³(x² + x¹ + 1) + 1(x² + x¹ + 1) = (x³ + 1) * (x² + x¹ + 1)
а)
т.к график проходит через начало отсчёта, то он график прямой пропорциональности вида: y=kx
Найдём точку, лежащую на графике с координатами (2;1). x=2, y=1
1=k×2
k=1:2
k=0,5
Этот график: y=0,5x
б)
График не проходит через начало отсчёта и он паралеллен оси абсцисс.
Следовательно:
Этот график вида: y=b, где b-некоторое число.
Судя по графику b=2.
Этот график: y=2
в)
График не проходит через начало отсчёта и он не паралеллен одной из осей. Следовательно он вида: y=kx+b
Точки пересечения: (0;3) и (2;0)
Подставим и получим:
3=k×0+b
0=k×2+b
Заметим, что в первом уравнении b=3. т.к k обратится в ноль.
Запишем в новом виде второе уравнение и получим:
0=k×2+3
2k=-3
k=-3:2
k=-1,5
Нашли все неизвестные переменные и уже, наконец, уравнение этого графика: y=-1,5x+3