А вы знали, что в природе всё не так просто устроено? Давайте посмотрим на количество лепестков у цветов. У ириса три лепестка, у крестовника тринадцать лепестков, у маргаритки их тридцать четыре, а у астры пятьдесят пять или восемьдесят девять. На первый взгляд это самые обычные числа, но давайте посмотрим на них повнимательнее. Несложно заметить, что перед нами ни что иное как числа Фибоначчи.
Числами Фибоначчи называют последовательность чисел, где каждое следующее число равно сумме двух предыдущих, а первые два - единицы. Посмотрим на первые несколько чисел. Это один, один, два, три, пять, восемь, тринадцать, двадцать один, тридцать четыре, пятьдесят пять, восемьдесят девять и так далее. Действительно, количество лепестков у цветов равно числам Фибоначчи.
Поэтому природа - это очень удивительная и сложная вещь!
№1
х2+5х-6=0
2x +5x - 6 = 0
7x - 6 = 0
7x = 6
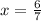
№2
Зх2+2х-1=0
6x+2x - 1=0
8x -1 = 0
8x=1
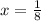
№3
х2-8х-84=0
2x-8x-84 =0
-6x - 84 = 0
-6x = 84
x = -14
№4
х2-5х+6=0
2x - 5x +6 =0
-3x+6 =0
-3x = -6
x= 2
№5
х2+4х+4=0
2x + 4x +4 = 0
6x +4 =0
6x = -4
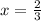
№6
2х2+3х+1=0
4x+3x+1 =0
7x+1 =0
7x = -1
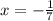
№7
4х2+10х-6=0
8x+10-6 =0
18x -6 =0
18x=6
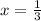
№8
3х2+32х+80=0
6x +32x +80 = 0
38x +80 =0
38x = -80
x = - 40/ 19
№9
х2=2х-48
2x = 2x - 48
0 = - 48
(утверждение ложно )
№10
–х2=5х-14
-2х = 5х - 14
-2х -5х = - 14
-7х = -14
х = 2
№11
х2+7х+2=0
2х+7х +2 = 0
9х +2 = 0
9х = -2
х = -2/9
№12
16х2-9=0
32х -9 = 0
32х = 9
х= 9/32
№13
–х2+х=0
-2х +х = 0
-х = 0
х = 0
№14
3х2-12х=0
6х-12х=0
-6х=0
х = 0
№15
х2+2х=0
2х+2х =0
4х =0
х=0
№16
-2х2+14=0
-4х+14=0
-4х= - 14
х= 7/2
№17
6х2=0
12х =0
х=0
№18
х2-64=0
2х-64=0
2х = 64
х= 32
№19
6х(2х+1)=5х+1
12х'2 +6х = 5х+1
12х'2 +6х -5х -1 = 0
12х'2+х -1 =0
12х'2 +4х -3х - 1 =0
4х (3х+1) - (3х+1) = 0
(3х+1) (4х - 1) =0
3х + 1 =0
4х-1 = 0
х = - 1/3
х= 1/4
№20
(х-2)2=3х-8
2х-4 = 3х - 8
2х - 3х = -8 +4
-х = -4
х= 4
буду благодарна, если ты нажмёшь на » и оценишь ответ как «лучший ». удачи ❤️
это точка и есть единственное решение неравенства, так как х^2, y^2 при любых значениях х и у принимают положительные значения или равны нулю, при х=0 и у=0, а значит и сумма х^2+ y^2 может быть больше или равно нулю, поэтому единственное решение этого неравенства
х=0
у=0
ответ: х=0, у=0