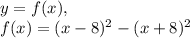
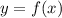— прямая пропорциональность.
— прямая пропорциональность, то есть доказать, что в выражении 
находится в первой степени 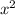(не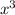 
, не 
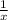, не 
и не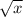 
, а просто ).. Если внимательно посмотреть это выражение можно видоизменить по формулам сокращенного умножения, а именно по формуле «разность квадратов». Действительно, данное выражение имеет вид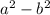 
, где 
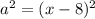, и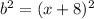 
. Формула «разность квадратов» раскрывается так: 
.
.
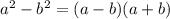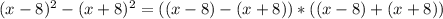
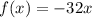, находится в первой степени, а значит зависимость — есть прямая пропорциональность. Доказано.
Рассмотрим функцию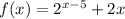
. Эта функция является возрастающей, как сумма двух возрастающих функций.
Теорема.
Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — число).
На рисунке видно, что графики пересекаются в одной точке, и при этом корень приближенный, трудно будет решить в стандартных решениях: