Какими свойствами обладает степень с дробным показателем (дробная степень)? Как выполнить возведение числа в дробную степень?
Определение.
1) Степенью числа a (a>0) с рациональным показателем r
где m — целое число, n — натуральное число (n>1), называется число
2) При a=0 и r>0
В частности,
При a<0 степень с дробным показателем не определяется.
Все свойства степеней из курса алгебры 7 класса выполняются и для степеней с рациональными показателями.
Для упрощения вычислений при возведении числа в дробную степень удобно использовать таблицу степеней и следующее свойство корня:
Тут вроде все понятно написано)
Ну и по примеру: 3+3^1/2 = 3+корень из 3
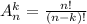
3. точка а расположена ближе к 0 если точки на координатной прямой расположены со стороны -, если точки расположены на координатной прямой со стороны +, то точка а должна быть удаленна дальше чем точка b что бы выражение a>b было верным.
4. если ты про символ <, то это не "не больше", а "менее"
5. если ты про символ >, то это не "не меньше", а"более"
6. данную форму записи нельзя назвать неравенством
7. данную форму записи нельзя назвать неравенством
8.неравенства , содержащие знаки >(больше) и < (меньше) называются СТРОГИМИ. Неравенства, содержащие знаки ≤(меньше или равно) и ≥
(больше или равно) называются НЕСТРОГИМИ.
Объяснение:
3. попробуй построить координатную прямую и нарисовать точки а и b так что бы а было больше b.
4. лично я не знаю как выглядит и изображается символ "не больше"
5. лично я не знаю как выглядит и изображается символ "не меньше"
6.данную форму записи нельзя назвать неравенством
7.данную форму записи нельзя назвать неравенством