Пусть х (км/ч) - скорость катера, тогда скорость катера по течению равна х+3 (км/ч), а против течения - х-3 (км/ч). Известно, что по течению катер проплыл 5 часов, в то время как против течения - 7 часов. Найдем пройденный путь для каждой ситуации:
S1 = (x+3)t1 - путь пройденный по течению, где t1 = 5ч
S2 = (x-3)t2 - путь пройденный против течения, где t2=7ч
Так как в обоих случаях пройден один и тот же путь, то S1 = S2. Приравняем их формулы и получим:
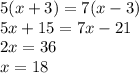
Таким образом, скорость катера в стоячей воде равна 18 км/ч.
По течению катер проплыл:
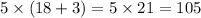
км
итак найдем же в каких тточках наша функция пересекает ось ох, тоест ьравна 0
y' = 6(x^2 + x - 2)
D = 1 +8 = 9
x1 = (-1 +3)/2 = 1
x2 = (-1-3)/2 = -2
Значит, на отрезке [-2;1] функция убывает. Значит наименьшее значение функции в тот самый момент, когда она перестаёт убывать, тоесть в 1
Y(min)=Y(1)= -8
С максимальным интереснее дело в том, что она сначала убывала, а потом стала возрастать нужно сравнить значения в граниных точках тоесть в х=2 и х=-1
Y(2)=3 Y(-1) = 12
ОТвет: Y(min) = -8 Y(max) = 12