1)ответ на фото
2)Треугольник АВС, угол В = 90, угол С = 60, АВ = 3√3 см
Угол А = 90 - 60 = 30
Напротив угла А = 30 лежит катет ВС вдвое меньше гипотенузы АС.
Пусть ВС = х, тогда АС = 2х
По теореме пифагора
4x^2 - x^2 = 27
3x^2 = 27
x^2 = 9
x = 3 cм - длина катета ВС
АС = 3 * 2 = 6 см.
ответ: 3 см, 6 см.
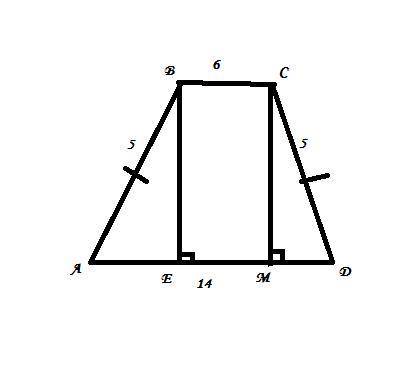
3)Так как трапеция равнобедренная, то AB=DC=5 см
EM=14-6=8cм⇒AE=MD=8÷2=4см
Теперь по Теореме Пифогора можем найти BE
AB²=AE²+EB²
BE=AB²-AE²(все под корнем)
ВЕ=5²-4²(всё под корнем)=√9=3 см
Sтрапеции=(BC+AD)÷2·BE
S=(6+14)÷2·3=30см²
ответ: 30 см².
(Чертёж в фото номер2)
4)пусть х меньшая сторона, а 4х большая
х*4х=36
х=3 см - меньшая сторона
3*3=9см кв площадь квадрата,построенного на меньшей стороне прямоугольника
Объяснение:
Удачи:)

ответ:Всего
Объяснение:Обратим внимание на то, что требуется сделать букет из 7 цветов так, чтобы в нем было хотя бы три красных тюльпана, а на количество белых тюльпанов ограничений нет. Тогда, заключаем, что в букете
1) в точности 7 тюльпанов;
2) наименьшее количество красных тюльпанов 3;
3) наибольшее количество красных тюльпанов 7.
По условию количество красных тюльпанов в саду 10, то все эти 3 пункта возможны. Обозначим белые тюльпаны через 0, а красные тюльпаны через 1. Так как порядок размещения не даёт новые то получаем следующие
0000111
0001111
0011111
0111111
1111111
Всего
Это квадратный двучлен. график этой функции - парабола ветвями вверх.
если дискриминант меньше нуля, те корней нет.
D = (2a +1)^2 - 4 *1*(- a/4) > 0;
4a^2 + 4a + 1 + a >0;
4a^2 + 5a + 1 > 0;
4(a+1)(a+ 0,25) > 0;
(-1)( - 0,25)a
a∈ ( -∞ ; - 1) U ( - 0,25;+ ∞)