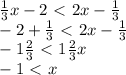
Среднее арифметическое- сумма всех множеств,деленная на кол-во значений:
1)Зайцев-
а)3+4+5+2+5+3+5+5= 32
32/8=4
Ср. ариф.- 4
б))Мода- наиболее часто встречающееся значение(повторяется):
3-4-5-2-5-3-5-5,как видим мода равна:
5
в) Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел:
3-4-5-2-5-3-5-5== 5-2=3
2)
Сидоров
а)3+2+2+3+3+3+3+3=22
22/8=2,75
Ср. ариф.- 2,75
б)
Мода:
3-2-2-3-3-3-3-3= 3
В) Размах ряда- 3-2=1
3)
Соколов
а)2+4+5+4+5+3=23
23/6=3,83
Ср. ариф- 3,83
б) Мода:
2-4-5-4-5-3= 4 ; 5 ( набор чисел может иметь не одну, а несколько мод)
В)
Размах ряда:
2-4-5-4-5-3= 5-2=3
№1 а=6
Объяснение:
используем теорему Виета для кубического уравнения
x₁ x₂ x₃ -корни уравнения х³+6х²+11х+а=0
x₁+x₂+x₃=-6 (1)
x₁x₂+x₂x₃+x₁x₃=11 (2)
x₁x₂x₃=-a (3)
т.к. корни образуют арифметическую прогрессию x₁=x₂-d x₃=x₂+d (4)
подставим (4) в (1) x₂-d+x₂+x₂+d=-6 3x₂=-6 x₂=-2
подставим (4) и значение x₂ в (2)
(-2-d)(-2)+(-2-d)(-2+d)+(-2)(-2-d)=11
4+2d+4-d²+4+2d=11 d²=1 d=-1 или d=1 подставим в (4), тогда данное уравнение имеет корни -3 -2 -1 подставим в (3)
(-3)(-2)(-1)=-а а=6
а) 2х - 3 > 3х + 1
2x-3x>1+3
-x>4
x<-4
x∈(-∞;4)
б) х(х + 2 ) > ( х + 3 )(х - 1)
x²+2x-x²+x-3x+3>0
3>0
x∈(-∞;∞)
в) х²-4х>(х-2)² .
x²-4x-x²+4x-4>0
-4>0
нет решения
2
a){3х+12>0 ⇒3x>-12⇒x>-4
{2х-3<0 ⇒2x<3⇒x<1,5
x∈(-4;1,5)
б){3х+2>2х-3⇒3x-2x>-3-2⇒x>-5
{x-5>0⇒x>5
x∈(5;∞)
3
А) х²-2х-3>0
x1+x2=2 U x1*x2=-3⇒x1=-1 U x2=3
x∈(-∞;-1) U (3;∞)
б) х²+4х+5<0
D=16-20=-4<0⇒при любом х выражение больше 0
ответ нет решения
в) х²-6х+9>0
(x-3)²>0
выражение больше 0 при любом х,кроме х=3
x∈(-∞;3) U (3;∞)
4
x²-12<0⇒(x-2√3)(x+2√3)<0⇒-2√3<x<2√3
1/3*x-2<2x-1/3
2x-1/3*x>-2+1/3
5/3*x>-5/3
x>-1
x=3