Найдите число погрешность приближения которого числом о,777 равна 0,008?

👇

Ответ:

09kok90

30.01.2020

A=?
b= $\frac{1}{125}$
a-b= $\frac{777}{1000}$
a= $\frac{1}{125}+ \frac{777}{1000}= \frac{157}{200}$
ответ: a= $\frac{157}{200}$ =0.785

4,5(68 оценок)

Открыть все ответы

Ответ:

tyrone12

30.01.2020

Биквадратное уравнение.

Решается заменой переменной:

x^2=t

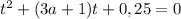
t^2+(3a+1)t+0,25=0

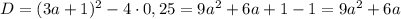
$D=(3a+1)^2-4\cdot 0,25=9a^2+6a+1-1=9a^2+6a$

Если D >0, т.е.

$9a^2+6a0\\\\3a(3a+2) 0$

$a\in (-\infty; -\frac{2}{3})U(0;+\infty)$

уравнение имеет корни:

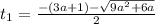$t_{1}=\frac{-(3a+1)-\sqrt{9a^2+6a} }{2}$ или $t_{2}=\frac{-(3a+1)+\sqrt{9a^2+6a} }{2}$

Обратный переход:

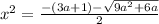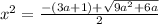
$x^2=\frac{-(3a+1)-\sqrt{9a^2+6a} }{2}$ или $x^2=\frac{-(3a+1)+\sqrt{9a^2+6a} }{2}$

Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку

Чтобы корни данного уравнения были равны,

с=0

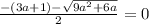
$\frac{-(3a+1)-\sqrt{9a^2+6a} }{2}=0$

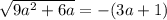
$\sqrt{ 9a^2+6a}=-(3a+1)$

Это иррациональное уравнение.

При (3a+1) >0 оно не имеет корней.

При (3а+1) ≤0

возводим обе части уравнения в квадрат:

9a^2+6a=9a^2+6a+1

0=1 - неверно, нет таких значений а

Аналогично

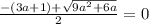
$\frac{-(3a+1)+\sqrt{9a^2+6a} }{2}=0$

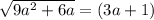
$\sqrt{ 9a^2+6a}=(3a+1)$

При (3a+1) < 0 оно не имеет корней.

При (3а+1) ≥0

возводим обе части уравнения в квадрат:

9a^2+6a=9a^2+6a+1

0=1 - неверно, нет таких значений а

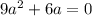
Если D=0 , т.е 9a^2+6a=0

a=0 или $a=-\frac{2}{3}$

При a=0

уравнение принимает вид:

x^4+x^2+0,25=0

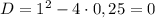$D=1^2-4\cdot 0,25=0$ ⇒ x^2=-1

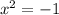
уравнение не имеет корней

При $a=-\frac{2}{3}$

уравнение принимает вид:

x^4-x^2+0,25=0

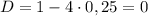$D=1-4\cdot 0,25=0$ ⇒ $x^2=\frac{1}{2}$

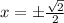
$x=\pm\frac{\sqrt{2} }{2}$

Уравнение 4-ой степени, значит

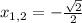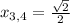
$x_{1,2}=-\frac{\sqrt{2} }{2}$ и $x_{3,4}=\frac{\sqrt{2} }{2}$

О т в е т. При $a=-\frac{2}{3}$

4,8(82 оценок)

Ответ:

queenames

30.01.2020

Объяснение:

Разложить число на простые множители значит записать число как произведение простых чисел .

Простым числом называют натуральное число , делящееся только на себя и на единицу. Составным числом называют число, имеющее больше двух различных делителей Например, числа 2,3,5,7, – простые, а числа 6(2*3),8(2*4),9(3*3) – составные.

Число 388 , оканчивается на 8 значит делится на 2

388:2=194, оканчивается на четное , значит также делится на 2

194 :2= 97 ,вспомним признаки делимости на 3 и 9 , число делится если сумма его цифр делится на 3 или 9.На четыре делится если 2 его последние цифры нули или образуют число которое делится на 4, На пять делится если число оканчивается на 5 или 0.осталось число 6 и 8. На 6 делится если одновременно делится на 2 и 3 , и число делится на 8, если три его последние цифры - нули или образуют число, которое делится на 8.

97=9+7=16, ни на одно число не делится, кроме 1 и самого себя значит 97 это простое число.

388=2*2*97

Число 2520

2520:2= 1260 ( признак делимости на 2)

1260:2=630 ( признак делимости на 2)

630:2=315 ( признак делимости на 5)

315:5=63 ( признак делимости на 3 и 9; 6+3=9 делится и на 3 и на 9

63:3=21 (2+1=3, признак делимости на 3 )

21:3=7 ( неделимое, простое число)

2520 = 2*2*2*3*3*5*7

2) Чтобы обратить обыкновенную дробь в десятичную, нужно числитель разделить на знаменатель.

3 2/5=17/5=17:5=3,4 мы получили конечную десятичную дробь, поскольку в знаменателе обыкновенной дроби стоит 5 ( получить конечную десятичную дробь можно если знаменатель обыкновенной дроби содержит простые множители 2 и 5)

43/30=43:30=1,4 33333… = 1,4(3), поскольку знаменатель обыкновенной дроби содержит кроме 2 и 5 еще 3, то она не может быть представлена конечной десятичной дробью.

4,8(70 оценок)

Это интересно:

Компьютеры-и-электроника

09.04.2021

Как блокировать доступ к YouTube для детей и сотрудников...

Компьютеры-и-электроника

27.01.2020

Изучаем, как создавать формы в HTML: полное руководство...

Хобби-и-рукоделие

14.04.2021

Завязывание скользящих узлов на ожерелье: профессиональный подход...

Образование-и-коммуникации