<!--c-->
Преобразим заданное уравнение:
x3+12x2−27x=a
С производной построим график функции y=x3+12x2−27x.
1. Введём обозначение f(x)=x3+12x2−27x.
Найдём область определения функции D(f)=(−∞;+∞).
2. Найдем стационарные и критические точки, точки экстремума и промежутки монотонности функции:
f′(x)=(x3+12x2−27x)′=3x2+24x−27.
Внутренние точки области определения функции, в которых производная функции равна нулю, назывём стационарными, а внутренние точки области определения функции, в которых функция непрерывна, но производная не существует, —критическими.
Производная существует всюду в области определения функции, значит, критических точек у функции нет. Стационарные точки найдем из соотношения f′(x)=0:
3x2+24x−27=0|÷3x2+8x−9=0D4=(b2)2−ac=822+9=25x1,2=−b2±D4−−√a=−82±25−−√1=−82±5x1=−82−5=−9x2=−82+5=1
Критические и стационарные точки делят реальную числовую прямую на интервалы с неизменным знаком производной. Чтобы определить знак производной, достаточно вычислить значение производной функции в какой-либо точке соответственного интервала.
Если производная функции в критической (стационарной) точке:
1) меняет знак с отрицательного на положительный, то это точка минимума;
2) меняет знак с положительного на отрицательный, то это точка максимума;
3) не меняет знак, то в этой точке нет экстремума.
Итак, определим точки экстремума:
При x<−9 имеем положительную производную (на этом промежутке функция возрастает); при −9<x<1 имеем отрицательную производную (на этом промежутке функция убывает). Значит, x=−9 — точка максимума функции. При −9<x<1 имеем отрицательную производную, при
Объяснение:
Число делится на 10 только в том случае, если оно оканчивается цифрой 0.
Посмотрим, какой цифрой оканчивается каждое слагаемое.
1) число 7 в разных степенях оканчивается разными цифрами. Попробуем установить закономерность.
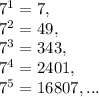
Т.е. последние цифры записи степеней семерки чередуются так: 7 - 9 - 3 - 1 и по кругу.
Т.к. 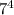 оканчивается цифрой 1, то
оканчивается цифрой 1, то 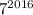 также оканчивается цифрой 1. Тогда число
также оканчивается цифрой 1. Тогда число 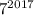 оканчивается цифрой 7.
оканчивается цифрой 7.
2) Для степеней четверки закономерность проще - 4 - 6 и по кругу:
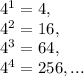
Поскольку 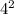 оканчивается цифрой 6, то
оканчивается цифрой 6, то 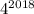 также оканчивается цифрой 6.
также оканчивается цифрой 6.
3) Закономерность для степеней тройки - 3 - 9 - 7 - 1 и по кругу:
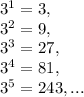
Т.к. 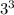 оканчивается цифрой 7, то
оканчивается цифрой 7, то 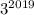 также оканчивается цифрой 7.
также оканчивается цифрой 7.
В итоге слагаемые 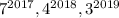 оканчиваются цифрами 7, 6 и 7 соответственно. Если их сложить, то в разрядке единиц класса единиц получим 0. Т.е. число
оканчиваются цифрами 7, 6 и 7 соответственно. Если их сложить, то в разрядке единиц класса единиц получим 0. Т.е. число 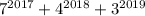 оканчивается цифрой 0 - следовательно, оно таки делится на 10.
оканчивается цифрой 0 - следовательно, оно таки делится на 10.
ОТВЕТ: да.
x²-4=0
x²=4
x=-2
x=2
x+5=0
x=-5
ответ x={-5;-2;2}