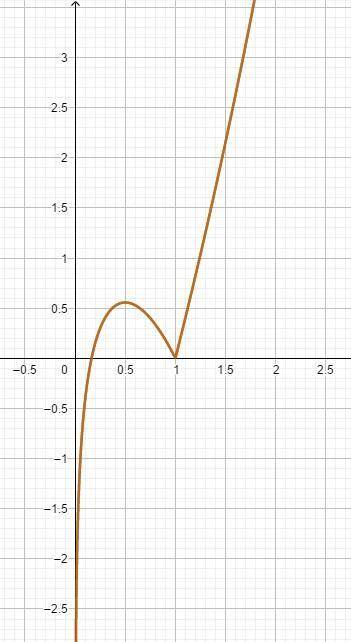
1) 6/a-1 2/a Общий знаменатель a(a-1)
2)2a²/3(a+1) 5x²/4(a+1) Общий знаменатель 12(a+1)
1)2c/5b-5c 3a²/35b²-35c² 7b/14b+14c
Чтобы подобрать общий знаменатель, нужно преобразовать выражения для удобства:
2c/5b-5c = 2c/5(b-c)
3a²/35b²-35c² = 3a²/35(b²-c²) = 35(b+c)(b-c)
7b/14b+14c = 7b/14(b+c)
Общий знаменатель (выражение, которое разделится на все знаменатели дробей по отдельности): 70(b+c)(b-c)
Проверка:
[70(b+c)(b-c)] : [5(b-c)] = 14(b+c)
[70(b+c)(b-c)] : [35(b+c)(b-c)] = 2
[70(b+c)(b-c)] : [14(b+c)] = 5(b-c), это дополнительные множители для числителей.
2) 5/4x-4 4x/1-x² 1/3x²+3x
Также, чтобы подобрать общий знаменатель, нужно преобразовать выражения для удобства:
5/4x-4 = 5/4(х-1)
4x/1-x² = 4х/-(x²-1) = -4x/(x+1)(x-1)
1/3x²+3x = 1/3x(1+x)
Общий знаменатель (выражение, которое разделится на все знаменатели дробей по отдельности): 12х(х+1)(х-1)
Проверка:
[12х(х+1)(х-1)] : 4(х-1) = 3x(x+1)
[12х(х+1)(х-1)] : (x+1)(x-1) = 12x
[12х(х+1)(х-1)] : 3x(1+x) = 4(х-1)
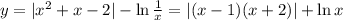
Область определения функции: x > 0
Рассмотрим два случая:
1) Если 0 < x < 1, то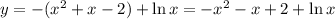 
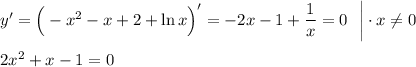
Получаем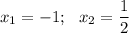 
, но рассматриваемая точка экстремума положительная, поэтому откидываем значение x = -1.
(0)__+___(1/2)____-___(1)
Вертикальная асимптота: x = 0 и учитывая то, что функция возрастает с 0(не включая) до значения x=1/2, то у функции наименьшего значения нет.
2) Если 1 < x ≤ 2, то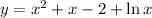 
- возрастает на промежутке x > 1. Но на промежутке x ∈ (1; 2] будет наибольшее значение функции в точке x = 2 и равно оно 
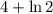. Наименьшего значения функции не существует.
