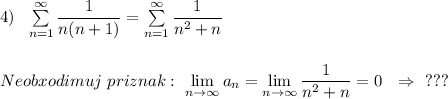
Если предел общего члена ряда равен 0, то ответ о сходимости ряда дать невозможно. Поэтому ряд надо исследовать с других признаков. (Вот если бы предел общего члена ряда не был = 0, то вывод можно было бы сделать однозначно, ряд бы расходился.)
Применим признак сравнения:
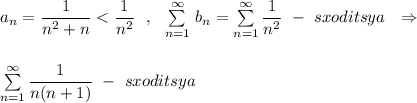
По признаку сравнения: мажорантный ряд сходится, значит сходится и минорантный ряд ⇒ исходный ряд сходится .
![6)\ \ \sum \limits _{n=1}^{\infty }\dfrac{1}{n}\cdot tg\dfrac{\pi}{3n}\\\\Neobx.\; priznak:\ \lim\limits _{n \to \infty} a_n= \lim\limits _{n \to \infty}\frac{1}{n}\cdot tg\frac{\pi}{3n}=\Big[0\cdot 0\; \Big]=0\ \ \Rightarrow \ \ \ ???\\\\sinx](/tpl/images/1344/7048/8accc.png)
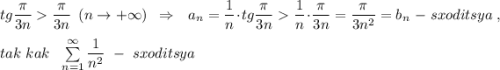
Получили, что сходится минорантный ряд, а из этого факта не следует сходимость мажорантного ряда. Поэтому применим признак сравнения в предельной форме.
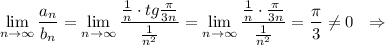
Оба ряда ведут себя одинаково, то есть сходятся .
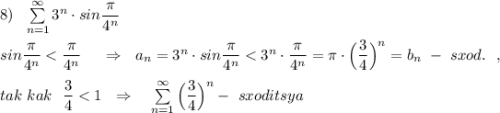
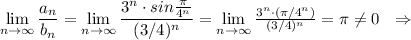
Оба ряда ведут себя одинаково, то есть сходятся .
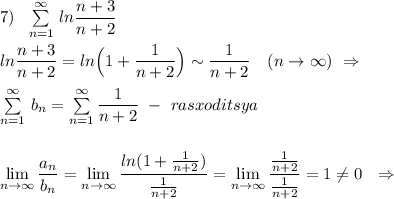
Оба ряда расходятся .
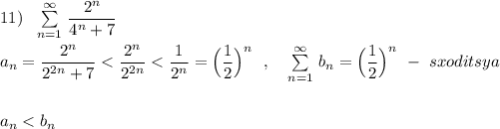
Оба ряда сходятся .
Если функция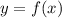 убывает, то при
убывает, то при 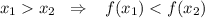 .
.
Если функция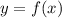 возрастает, то при
возрастает, то при 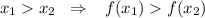 .
.
a)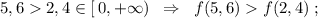
г)![-2,8-7,3\in (-\infty ,0\, ]\; \; \Rightarrow \; \; f(-2,8)](/tpl/images/0642/2527/dfcd2.png) ;
;
б) так как заданная функция чётная и симметрична относительно оси ОУ, то значения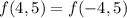 .
.
в) из-зa чётности функции имеем: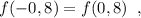
из-за возрастани функции имеем: