Объяснение:
0,0036=3,6 * 10¯³
если мы в записи числа 3,6 передвинем запятую влево на 3 цифры(т.е умножаем на 0,001),то вместо числа 3,6 получим 0,0036
давай еще пару примеров
0,045 =4,5 *10¯² передвинули запятую на 2 цифры(т.е умножаем на 0,01)поэтому 10 в минус 2 степени
0,000079=7,9*10¯⁵ передвинули запятую на 5 цифр(т.е умножаем на 0,00001),поэтому 10 в минус 5 степени
теперь немного другие примеры
7900000=7,9*10⁶ здесь запятую будем переносить вправо на 6 цифр(т.е умножаем на 1 000 000) поэтому 10 в 6 степени
2700=2,7*10³; 95000=9,5*10⁴; 420000000=4,2*10⁸
2.
А¹⁰*А⁻⁷=А¹⁰⁺⁽⁻⁷⁾=А³ здесь действительно должно быть плюс 3(при умножении степеней с одинаковым основанием показатели складываются)
3 задание смотри внизу.
а вот Условие 4) и 5 ) заданий не понятно записаны.
в 4)если надо решить уравнение √х = 3 то тогда получим ответ х=9,а если х²=3 то тогда х1 =- √3, х2=√3
и 5) 2/2√3 = 2√3/2 √3:√3= 2 √3/2 √3² ( тут сокращение) =√3/3 и тут не понятно,какое именно задание,похоже,что надо избавиться от корня в знаменателе.Если это так,напиши,я редактирую ответ и объясню и эти задания
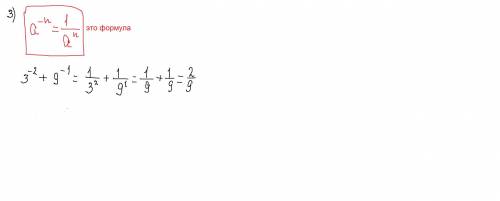
Пусть х - любое натуральное число, тогда следующее натуральное число будет на 1 больше и так далее. Запишем пять последовательных натуральных чисел, первое из которых х: х, х + 1, х + 2, х + 3, х + 4.
Найдем сумму этих пяти чисел:
х + (х + 1) + (х + 2) + (х + 3) + (х + 4) = 5 * х + 10 = 5 * (х + 2).
Как известно произведение делятся на число 5, если хотябы один из множителей делится на число 5. Так как 5 : 5 = 1, значит последовательность пяти натуральных чисел делится нацело на 5, что и требовалось доказать.
Объяснение:)
Тождество – это равенство, верное при любых значениях переменных; любое верное числовое равенство – это тоже тождество.
Для 8-го класса вводится уточненное определение:
Тождества – это верные числовые равенства, а также равенства, которые верны при всех допустимых значениях входящих в них переменных.
Такие разные определения даются потому, что в 8 классе появляются выражения, которые уже имеют смысл не для всех значений переменных, а только для значений из их ОДЗ.
Вообще, тождество – это частный случай равенства. То есть, любое тождество является равенством. Но не всякое равенство является тождеством, а только такое равенство, которое верно для любых значений переменных из их области допустимых значений.
Знак тождества ≡
Примеры:
Тождествами являются числовые равенства вида 2+3 = 5 и 7−1 = 2*3,
так как эти равенства являются верными.
То есть, 2+3 ≡ 5 и 7−1 ≡ 2*3.
Равенство 3*(x+1)=3*x+3.
При любом значении переменной x записанное равенство является верным в силу распределительного свойства умножения относительно сложения, поэтому, исходное равенство является примером тождества.
А вот равенство (a+2)*b=(b+2)*a не является тождеством, так как существуют значения переменных, при которых это равенство будет неверным.
Равенство (a + 2)*b = (b + 2)*a обратится в неверное равенство, если взять любые различные значения переменных a и b.
К примеру, при a = 0 и b = 1 мы придем к неверному равенству
(0 + 2)*1= (1 + 2)*0.
Равенство |x| = x, где |x| - модуль переменной x, также не является тождеством, так как оно неверно для отрицательных значений x.
Примерами наиболее известных тождеств являются основное тригонометрическое тождество вида sin²α + cos²α = 1 и основное логарифмическое тождество