 ;
;
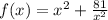 ;
;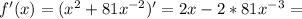
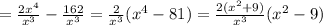 ;
;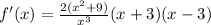 ;
;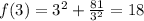 ;
;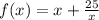 ;
;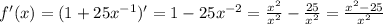 ;
;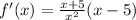 ;
;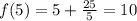 ;
;Необходимо доказать, что:
(x+3)*(x+6)*(x+2)*(x+1)>96*x^2
При условии: x>0
Умножим первую скобку на третью, а вторую на четвёртую:
(x^2+5x+6)*(x^2+7x+6)>96*x^2
Поделим обе части неравенства на x^2 , причём каждую из полученных скобок поделим почленно на x. Поскольку x^2>0 , то неравенство не меняет знак.
Имеем:
(x+ 5+ 6/x)*(x + 7 +6/x)>96
Сделаем замену : x+6+6/x=t
(t-1)*(t+1)>96
t^2-1>96
t^2>97
Необходимо доказать , что t^2>97
Поскольку x>0 , то можно применить неравенство о среднем арифметическом и среднем геометрическом:
x+ 6/x >= 2*sqrt(x *6/x)=2*sqrt(6)
Откуда:
t= x+6 +6/x>= 6+2sqrt(6)
t^2>=(6+ 2sqrt(6) )^2=36+24+24*sqrt(6)
=60+24*sqrt(6)>60+24*sqrt(4)=
=60+48=108>97
Таким образом мы показали что:
t^2>97, а значит мы доказали , что неравенство:
(x+3)*(x+6)*(x+2)*(x+1)>96*x^2 выполняется при любом x.
Что и требовалось доказать.
Более того , мы может даже усилить данное неравенство , сделав его строгим и найти наибольшее целое число , что может усилить данное неравенство.
t^2-1>= (6+ 2sqrt(6) )^2-1=59+24sqrt(6)
(x+3)*(x+6)*(x+2)*(x+1)>=(59+24sqrt(6))*x^2
24*sqrt(6)=sqrt(24^2 *6)=sqrt(3456)
sqrt(3364) <sqrt(3456) < sqrt(3481)
58 <24*sqrt(6)<59
59+24sqrt(6) >59+58=117
Наибольшее усиление для сравнения с целым числом:
(x+3)*(x+6)*(x+2)*(x+1)>117*x^2
n=25 - количество выпускников
25*(25-1)/2= 25*24/2= 300 - количество рукопожатий
25*24 = 600 (шт.) - количество заказанных фотографий
Пояснение:
Каждый из 25 выпускников руку 24-м остальным выпускникам. Но, произведение 25*24 = 600 даст нам удвоенное число рукопожатий (т.к. первый руку второму, а затем второй первому, на самом же деле это одно рукопожатие). Поэтому полученный результат делим на 2 и получаем ответ.