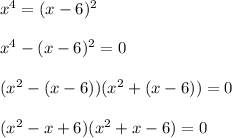
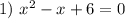
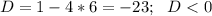- корней нет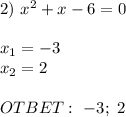
Пусть х грамм масса одного вещества, а у грамм второго. Так как масса смеси, состоящей из двух вещество равна 900г, получим первое уравнение: х + у = 900. Тогда после того, как из этой смеси взяли первого вещества и 70% второго, в ней осталось первого вещества на 18г меньше, чем второго, получим следующее уравнение: (у - 70%у) - (х - 5/6х) = 18.
Необходимо найти остаток смеси х и остаток смеси у.
Найдём значение "х" и "у".
(у - 70%у) - (х - 5/6х) = 18 ;
100% - 70 % = 30 %;
Преобразуем уравнение:
30%у - 1/6х = 18;
3/10у - 1/6х = 18;
Найдём общий знаменатель:
3/10у * 6 - 1/6х * 10 = 18 * 60;
18/60у - 10/60х = 1080/60;
Сокращаем дроби:
18у - 10х = 1080;
10х = 18у - 1080;
Сокращаем на 10:
х = 1,8у - 108;
Теперь подставим значение х в первое уравнение, получим:
900 = х + у;
х = 900 - у;
х = 1,8у - 108;
900 - у = 1,8у - 108;
-2,8у = - 1008;
Упрощаем выражение:
-2,8у * (-1) = - 1008 * (-1);
2,8у = 1008;
у = 360 грамм;
х = 540 грамм;
Найдём остаток от "х" и "у".
у - 70%у = 0,3у = 0,3 * 360 = 108 грамм (столько осталось смеси у);
х - 5/6х = 1/6х = 1/6 * 540 = 90 грамм (столько осталось смеси х) ;
Проверяем:
После того, как из смесей выделили определенное количество, смесь у осталось на 18 грамм больше, чем смеси х.
Из этого следует:
(у - 70%у) - (х - 5/6х) = 18;
Подставляем значения:
108 - 90 = 18 ;
18 = 18 (Значения найдены верно);
ответ: Первого вещества осталось 90 грамм, а второго вещества осталось 108 грамм.
Расстояние, которое должен проплыть второй второй пловец, до того момента, как он догонит первого пловца обозначим через S. Тогда второй пловец проплывёт S - 70м. Плыть они будут одно и то же время. Значит:
S/80 = (S - 70)/45;
45S = 80S - 5600;
S = 160м;
t = 160/80 = 2 мин.
Аналогично для скорости 52м/сек:
S/520 = (S - 70)/45;
45S = 52S - 3640;
S = 520м;
t = 520/52 = 10 мин, т.е. сможет догнать.
А вот сможет ли второй пловец догнать первого, если он будет плыть с такой же скоростью, как и первый - это навряд ли, это и так понятно.
