Решим дискриминант и после этого сделаем метод интервала.
x²-3x-4 < 0
Дискриминант:
x²-3x-4 = 0
D = b²-4ac => (-3)²-4*1*(-4) = 9+16 = 25 > 0, 2 корня.
√25 = 5 (можно и в уме)
x =
x₁ =
x₂ =
Корни уравнения: (x+1)(x-4)
На графике будет выглядеть так:
-∞ + - + +∞
00>
-1 4 x
Воспользуемся методом интервала, чтобы понять, в какое направление пойдёт решение:
f (x) = (x+1)(x-4)
f (2) = (2+1)(2-4) = 3*(-2) = -6
ответ: (-∞;-1) ∪ (4;+∞).
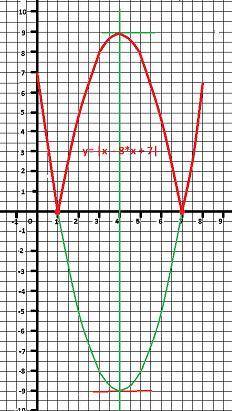
Дано: y = |x² - 8*x + 7|
Объяснение:
Сначала решаем квадратной уравнение:
a*x² + b*x + c = 0
Вычисляем дискриминант - D.
D = b² - 4*a*c = -8² - 4*(1)*(7) = 36 - дискриминант. √D = 6.
Вычисляем корни уравнения.
x₁ = (-b+√D)/(2*a) = (8+6)/(2*1) = 14/2 = 7 - первый корень
x₂ = (-b-√D)/(2*a) = (8-6)/(2*1) = 2/2 = 1 - второй корень
7 и 1 - корни уравнения - нули функции.
Вершина посередине между нулями - х=4.
Уmin(4) = - 9 - этот минимум надо перевернуть в +9.
Рисунок с графиком в приложении.
Строим параболу и отрицательную часть отражаем относительно оси ОХ.