Прочтите текст. наталкинское золоторудное месторождение — золоторудное месторождение, находящееся в тенькинском районе магаданской области на площади яно-колымской складчатой системы. расположено в 390 км от магадана в долине р. омчак между ручьями геологический и глухарь. месторождение относится к золото-кварцевым объектам штокверкового типа. рудное поле наталкинского месторождения площадью 40 км2 в составе омчакского золоторудного узла расположено в зоне тенькинского (омчакского) глубинного разлома. сложено нижне- и верхнепермскими осадочными , претерпевшими воздействие регионального динамо-термального метаморфизма на уровне зеленосланцевой фации. интрузивные образования представлены дайками и силами спессартитов и риолитов раннемелового возраста. оруденение контролируется серией продольных разломов и выражено мощными протяженными зонами жильно-прожилковой минерализации. руды месторождения относятся к арсенопиритовому минеральному типу. запасы 1260 т. среднее содержание золота в запасах руд месторождения наталка на 2017 год составляет 1,7 г/т. предположим, что ювелирный завод хочет выпустить партию из 1000 сережек 585 пробы весом в 3 грамм. хватит ли 1000 тонн руд наталкинского месторождения для сережек? ответ обоснуйте. пробой в ювелирных изделиях называют процентное содержание драгоценных металлов. например, в серьгах 585 пробы содержится 58,5% золота.
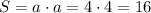

Пояснение:
Это квадратное уравнение можно решить сразу тремя : через теорему Виета и через Дискриминант (полный и краткий). Покажу все три.
(теорема Виета)
- можно применять, если первый (старший) коэффициент (а) равен единице (1), то есть квадратное уравнение имеет вид:
x² ± px ± q = 0.
x² + 8x + 15 = 0
p = 8; q = 15.
По т. Виета:
x₁ + x₂ = - 8,
x₁ × x₂ = 15.
x₁ = - 5,
x₂ = - 3.
<><><><><><><><><><><><><><><><>
IIа (Дискриминант)
- можно применять к любым полным квадратным уравнениям вида:
ax² ± bx ± c = 0.
x² + 8x + 15 = 0
a = 1; b = 8; c = 15.
D = b² - 4ac = 8² - 4 × 1 × 15 = 64 - 60 = 4 = 2².
D > 0 (значит, уравнение имеет два действ. корня)
x₁ = - 4 - 1 = - 5,
x₂ = - 4 + 1 = - 3.
<><><><><><><><><><><><><><><><>
IIб ("краткий" Дискриминант)
- можно применять к любым полным квадратным уравнениям вида:
- можно применять к любым полным квадратным уравнениям вида:ax² ± bx ± c = 0,
где b - чётное число (то есть делится на 2 без остатка).
x² + 8x + 15 = 0
a = 1; b = 8; c = 15.
k = b ÷ 2 = 8 ÷ 2 = 4.
D₁ = k² - ac = 4² - 1 × 15 = 16 - 15 = 1.
x₁ = - 4 - 1 = - 5,
x₂ = - 4 + 1 = - 3.
<><><><><><><><><><><><><><><><>
ответ: - 5; - 3.
Удачи Вам! :)