№1
Пусть x-скорость лодки по течению, тогда y-скорость лодки против течения. Составим систему уравнений:
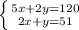
Домножим нижнее уравнение на -2
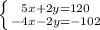
Решим методом сложения:
5x+2y-4x-2y=120-102
x=18
Подставим значение х во второе уравнение и найдем y:
2*18+y=51
36+y=51
y=51-36
y=15
Пусть скорость течения-x, а скорость лодки - y. Составим систему уравнений:
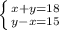
Решим методом сложения
x+y+y-x=32
2y=32
y=32/2
y=16
Подставим значение y в первое уравнение и найдем x:
x+16=18
x=18-16
x=2
ответ: скорость течения реки- 2км/ч. скорость лодки - 16 км/ч
№2
Пусть x- возраст отца, y-возраст сына
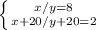
Выразим x из первого уравнения:
x/y=8
x=8y
Подставим значение x во второе уравнение:
8y+20/y+20=2
Перемножим методом креста:
2y+40=8y+20
-6y=-20
y=20/6
Выразим x:
x=8*20/6
x=80/3
Прибавим по 20 к x и y
x+20=80/3+20=140/3=46
y+20=20/6+20=140/6=23
ответ: Сыну 23 года, Отцу 46 лет.
Объяснение:
Если строить одну пристань в точке X, то оптимальному её расположению соответствует такая точка, для которой AX+XB минимальна. Эта точка находится так: отражаем B симметрично относительно реки, получая точку B', и проводим отрезок AB'. В пересечении с рекой и получается X. Ввиду равенства XB=XB', а также неравенства треугольника AX+XB'<=AB, получаем нужный вывод.Пусть река идёт по горизонтали, и это ось абсцисс. Тогда ординаты точек A и B отличаются на 3. Расстояние равно 5, и тогда абсциссы отличаются на 4 в силу теоремы Пифагора. Разность абсцисс у точек A, B' такая же, а разность ординат равна 2+5=7. Это значит, что сумма длин дорог равна AX+XB=AB'=корень из(7^2+4^2}=корень из(65) < 8,1, что проверяется возведением в квадрат. Тогда в лимит 10,1 с учётом стоимости постройки одной пристани мы укладываемся.