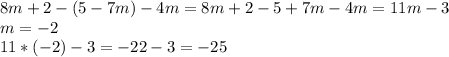
Уравнение касательной y = f ’(x0) · (x − x0) + f (x0)
Здесь f ’(x0) — значение производной в точке x0, а f (x0) — значение самой функции.
Значение функции в точке х = 2:
f(2) = 2-3*2² = 2-12 = -10.
Производная функции равна f'(x) = 1-6x.
В точке Хо = 2 её значение f'(2) = 1-6*2 = -11.
Уравнение касательной: у = -11(х-2)-10 или, раскрыв скобки,
у = -11х+22-10 = -11х+12.
B2) Даны уравнения функции y=0,5x^4-x и касательной к её графику
y=-(3/4)x-(3/32).2
Объяснение:
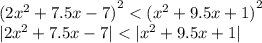
Рассмотрим 4 случая, когда выводим выражения из модулей:
1) 1ое и 2ое выражения положительные
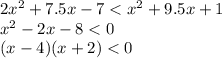
т.е. ответ -1+0+1+2+3=5
2) 1ое положительное и 2ое отрицательное

т.е. ответ -5-4-3-2-1+0=-15
3) 1ое отрицательное и 2ое положительное
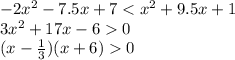
т.е. область будет лежать в окрестностях (-бесконечность;-6) и (1/3;+бесконечность) в ответе сумма всех целых чисел: 1+2+3+4+5=15 т.к. остальные числа взаимно сокращаются
4) 1ое и 2ое отрицательные
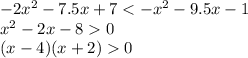
т.е. область в окрестностях (-бесконечность;-2) и (4;+бесконечность). В ответе сумма всех целых чисел дает: -3 аналогично
Тогда, если суммировать все ответы в 4 случаях: 5-15+15-3=2