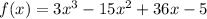
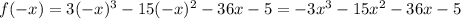
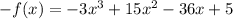
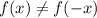 и
и 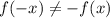 , то функция является функцией общего вида.
, то функция является функцией общего вида.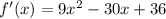
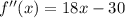
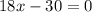
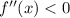
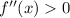
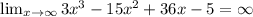
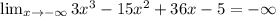
Сначала приравняем к 0
z² + 6z - 7 = 0
D = (6)² - 4 * 1 * (-7) = 36 + 28 = 64
По теореме Виета:
z1 + z2 = -6
z1 * z2 = -7
z1 = -7
z2 = 1
Переформулируем под вид a(x-x1)(x-x2)..., имея уже корни
1*(x-(-7))(x-1) ≤ 0
Там надо нарисовать прямую и отметить на ней точки -7 и 1. И подставлять под х в уравнении наверху сначало число больше 1, потом больше -7 и меньше 1 (0, например), а в конце меньше -7. Затем над отрывками, откуда брались числа, пишешь +, если результат слева положительный, и -, если наоборот.
Могу показать на фото. Я сделала, у меня получился ответ: x принадлежит [-7; 1]
Объяснение:
(t-32)F(t+1)=tF(t).
Подставим в него t=0, получим -32F(1)=0*f(0), откуда F(1)=0.
Подставим t=1, получим -31F(2)=F(1)=0, т.е. также F(2)=0.
Затем подставляем последовательно t=2,3,...,31. Будем последовательно получать, F(3)=F(4)=...=F(32)=0.
Если дальше подставить t=32, то получится опять 0=F(32).
Дальнейшая подстановка t=33, не позволяет найти F(33), т.к. будет F(34)=33F(33). Аналогично, подстановкой t=-1, мы найдем -33F(0)=-F(-1), откуда не найти ни F(0) ни F(-1). Таким образом, пока установлено, что F(t) имеет корни 1,2,3,..., 32, а значит, он делится на (t-1)(t-2)·...·(t-32). Поэтому возникает предположение, что F(t) можно попробовать искать в виде
F(t)=с(t-1)(t-2)·...·(t-32), где c - некоторая константа. Покажем, что этот F(t) действительно удовлетворяет тождеству:
(t-32)F(t+1)=(t-32)·ct(t-1)·...·(t-31)=t·c(t-1)·...·(t-31)(t-32)=tF(t). Итак, некоторые F(t) найдены. Значит, в качестве R(x) можно взять, например
R(x)=63³²F(x/63)=(x-63)(x-2·63)(x-3·63)·...·(x-32·63).