Объяснение:
1. Решим задачу с арифметической прогрессии. По условию нам дано, что первый член прогрессии равен 7, её разность равна 1 (последовательные натуральные числа), а сумма n членов прогрессии равна 150. По формуле суммы n членов прогрессии, найдем количество чисел:
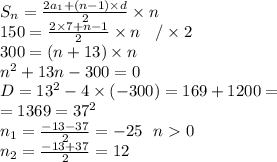
n = 12
ответ: 12
2.
По условию нам дано, что первый член прогрессии равен 20, её разность равна 2 (последовательные четные натуральные числа), а сумма n членов прогрессии равна 120. По формуле суммы n членов прогрессии, найдем количество чисел:
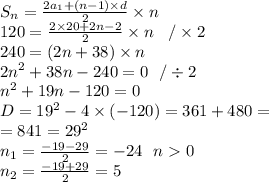
n = 5
ответ: 5
x²+2x+10=4x²-4x+1
x²+2x+10-4x²+4x-1=0
-3x²+6x+9=0
3x²-6x-9=0
x²-2x-3=0
x=3 и х=-1