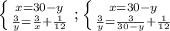
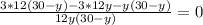
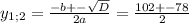
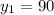не подходит, т.к. y<30
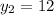км/ч скорость второго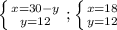
Объяснение:
Что такое возрастание или убывание функции? Объясняем на примере. Пусть у нас есть функция y=2x. Начнем подставлять в нее значения х, и вычислять значения у:
x₁=-1; y₁=2*(-1)=-2;
x₂=-0.5; y₂=2*(-0.5)=-1;
x₃=0; y₃=2*0=0;
x₄=1; y₄=2*1=2.
Смотрим на полученные числа. Видим, что x₄>x₃>x₂>x₁ при этом y₄>y₃>y₂>y₁. Т.е. значения х возрастают от x₁ до x₄, при этом значения у также возрастают от y₁ до y₄. Такая функция называется возрастающей (возрастает х → возрастает у).
Пример убывающей функции: y=-3x.
x₁=-1; y₁=-3*(-1)=3;
x₂=-0.5; y₂=-3*(-0.5)=1.5;
x₃=0; y₃=0;
x₄=1; y₄=-3*1=-3.
Видим, что х возрастает от -1 до +1, а у при этом убывает от +3 до -3 (возрастает х → убывает у). Такая функция называется убывающей.
Но т.к. мы не можем перебрать все значения х (их же бесконечно много) чтобы убедиться, что функция ведет себя одинаково на всей числовой прямой даже для таких простых функций, как в примере (такие функции называются линейными, и на графике они предстваляют собой прямую линию, а бывают еще и более сложные функции, которые возрастают на одном интервале, а на другом убывают), математики нашли универсальный определения возрастания или убывания функции.
Это определение через производную функции: если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X; если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X.
1. y=2x+3;
найдем производную этой функции:
y'=(2x+3)'=2x'+3'=2+0=2';
y'=2.
Производная больше нуля, мало того: производная вообще не зависить от х. Следовательно функция возрастающая при любом х, говорят: "функция возрастает на интервале от минус бесконечности до плюс бесконечности".
y=2x+3 возрастает на Х ∈ (-∞;+∞).
* График этой функции - прямая, проходящая через две точки: (0;3) и (-3/2;0) Легко построить.
2. y=1-3x;
производная этой функции:
y'=(1-3x)'=0-3=-3 < 0
Здесь производная меньше нуля при любых значениях х (производная - постоянная величина). Функция убывает при любом х.
y=1-3x убывает на Х ∈ (-∞;+∞).
** График этой функции - прямая, проходящая через две точки: (0;1) и (1/3;0)
3. y=3-x²;
производная функции:
y'=(3-x²)'=0-2x=-2x.
Здесь производная зависит от значения х. Мало того: существует точка, где производная равна 0:
y'=0; -2x=0; x=0.
Эта точка называется точкой экстремума. Эта точка "отделяет" интервалы возрастания функции от интервалов убывания.
Получаем два интервала, на которых функция ведет себя совершенно по-разному. Если на одном она возрастает, то на другом убывает.
Эти интервалы:
x∈(-∞;0) и x∈(0;+∞);
Проверим. Возмем первый (левый) интервал x∈(-∞;0) , подставим два каких-либо (любых) числа х из этого интервала, и вычислим значение функции у:
x=-2; y=3-(-2)²=3-4=-1;
x=-1; y=3-(-1)²=3-1=2;
х возрастает (от-2 до -1), при этом у возрастает (от -1 до +2) - функция возрастает на интервале x∈(-∞;0).
Возмем правый интервал x∈(0;+∞), подставим два каких-либо числа х из этого интервала, и вычислим значение функции у:
x=2; y=3-(2)²=3-4=-1;
x=3; y=3-(3)²=3-9=-6;
х возрастает (от 2 до 3), у убывает (от -1 до -6) - функция убывает на интервале x∈(0;+∞).
*** График этой функции - квадратичная парабола y=x², "перевернутая вверх ногами" с вершиной в точке (0;3), пересекает ось ОХ в точках (-√3;0 ) и (√3;0).
2)9a2
3)-125x3
4)100a2b2
5)0,0016x4y4
6)-0,125b3d3