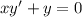
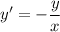 - уравнение с разделяющимися переменными
- уравнение с разделяющимися переменными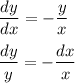
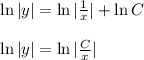
 - общее решение
- общее решение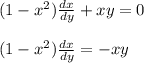

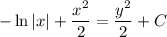 - общий интеграл
- общий интеграл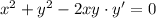

 , тогда
, тогда 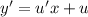



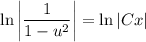
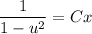
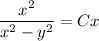 - общий интеграл
- общий интеграл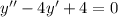
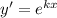 , тогда будем иметь характеристическое уравнение следующего вида:
, тогда будем иметь характеристическое уравнение следующего вида:
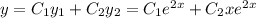 - общее решение
- общее решение
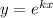 , тогда получаем
, тогда получаем
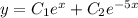

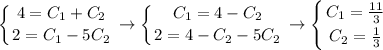
 - частное решение
- частное решение
АС=204 км.
Объяснение:
Расстояние между городами А и В равно 348 км. Из города А в город В выехал автомобиль, а через 1 час следом за ним со скоростью 85 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он вернулся в А, автомобиль прибыл в В. Найдите расстояние от А до С.
Формула движения: S=v*t
S - расстояние v - скорость t – время
85 (км/час) - скорость мотоциклиста.
АС/85=t – время мотоциклиста от А до С.
CA/85=t – время мотоциклиста от С до А.
t+t=2t = всё время мотоциклиста.
АС=СА=85*t= - расстояние мотоциклиста.
2t+1 – время автомобиля (мотоциклист выехал позже на 1 час).
CВ=348-AС=348 -85t – расстояние автомобиля от С до В.
348/(2t+1) - скорость автомобиля.
C этой скоростью автомобиль проехал путь СB за t часов (так как автомобиль и мотоцикл были в пути от С до В одинаковое время=t).
Уравнение:
[348/(2t+1)]•t=348-85t
(348*t)/(2t+1)=348-85t
Умножить уравнение на (2t+1), чтобы избавиться от дроби:
348t=(348-85t)(2t+1)
348t=696t+348-170t2-85t
Привести подобные члены:
170t²-263t-348=0, квадратное уравнение, ищем корни:
D=b²-4ac =69169+236640=305809 √D=553
t₁=(-b-√D)/2a
t₁=(263-553)/340=290/340=0,85 – отбрасываем, как не отвечающий условию задачи.
t₂=(-b+√D)/2a
t₂=(263+553)/340
t₂=816/340
t₂=2,4 (часа).
По условию задачи необходимо вычислить АС.
АС=85*t
АС=85*2,4=204 (км).
В ЧИСЛИТЕЛИ БУДЕТ 16 И ЭТИ КОРНИ А В ЗНАМЕНАТЕЛИ ЭТИ ЧИСЛА ТОЛЬКО БЕЗ КОРНЯ