Відповідь:
Воспользуемся формулой
1) sin72°cos18°+sin18°cos72°
sin(а+b)=sin a*cos b+cos a* sin b
sin (72°+18°) = sin 90° = 1
2) cos81°cos21°+sin81°sin21°
3) cos15+cos75 = cos (15+75)= cos 90 = 0
4) sin 7 α - sin α = sin (7 α - α) = sin 6 α
5) cos 20 * cos 40
нужно умножить выражение на sin20, чтобы получился синус двойного угла, и тут же разделить это выражение. Думаю, если оставить все на словах, вы мало поймете, хорошо, запишу: cos20 * cos40 =1(2sin20*cos20)*cos40= 1*sin40*cos40*cos80/sin20
В общем, суть такая.
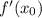производная функции в данной точке. А 
точка касания по иксу.
мы должны найти производную общего типа этой функции.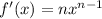
- где n это степень.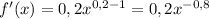
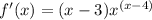
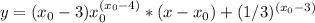
и получаешь уравнение касательной.
(√20 - 10√5) * √5 = (√4*5 - 10√5) * √5 = (2√5 - 10√5) * √5 = -8√5 * √5 = -8 * 5 = -40,
(13 - √6)² = 13² - 2*13*√6 + (√6)² = 169 - 26√6 + 6 = 175 - 26√6