1) обозначив 2^x = z, получим квадратное уравнение относительно z
z^2 - (7-x)*z + 12-4x = 0
D = (7-x)^2 - 4*(12-4x) = 49 - 14x + x^2 - 48 + 16x = 1 + 2x + x^2 = (x+1)^2
z1 = (7-x + |x+1|)/2 ___ z2 = (7-x - |x+1|)/2
--- x+1 >= 0 или x >= -1
z1 = (7-x + x+1)/2 ___ z2 = (7-x - x-1)/2
z1 = 4 ___ z2 = 3 - x
2^x = 4 ___ 2^x = 3 - x
x1 = 2 ___ x2 = 1
(решение второго уравнения 2^x = 3 - x можно объяснить графически...
функция 2^x строго возрастает, функция 3 - x строго убывает (график---прямая линия), пересечение графиков этих функций---единственная точка...)
--- x+1 < 0 или x < -1
z1 = (7-x + (-(x+1)))/2 ___ z2 = (7-x - (-(x+1)))/2
z1 = (7-x -x-1)/2 ___ z2 = (7-x + x+1)/2
z1 = 3 - x ___ z2 = 4
2^x = 3 - x ___ 2^x = 2^2
здесь пустое множество решений, т.к. было условие x < -1
ответ: x = 1 или x = 2
2) нужно постараться свести уравнение к одному основанию и к одному показателю степени...
5^(x^2) + 7^(x^2) / 7 - 7^(x^2) + 5^(x^2)*17 / 25 = 0
5^(x^2) * (1+17/25) - 7^(x^2) * (1- 1/7) = 0
5^(x^2) * (42/25) = 7^(x^2) * (6/7)
5^(x^2) / 7^(x^2) = (6/7) / (42/25)
(5/7)^(x^2) = (6*25) / (7*42)
(5/7)^(x^2) = 25/49
x^2 = 2
x = + - корень(2)
а) n-ый член геометрической прогрессии ищется по формуле:
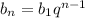
Тогда пятый член этой прогрессии равен:

б) Аналогично по формуле n-го члена геом. прогрессии вычисляем девятый член прогрессии:
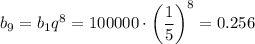
в) Сумма первых n членов геометрической прогрессии ищется по следующей формуле:
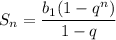
Тогда сумма первых восьми членов этой прогрессии равна:

г) Аналогично с в) по формуле суммы n первых членов геометрической прогрессии вычисляем сумму первых пяти членов этой прогрессии:
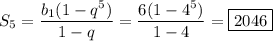
д) Предполагается, что нужно найти сумму бесконечно убывающей геометрической прогрессии:

Тогда
А) -36; - 12; -4;
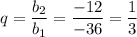
Сумма бесконечно уб. г.п. 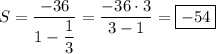
Б) 
Сумма бесконечно убывающей геометрической прогрессии:
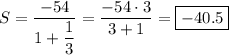
e) используя n-ый член геометрической прогрессии, рассмотрим пятый член этой прогрессии:
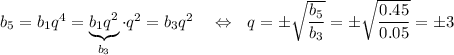
Так как по условию q>0, то q=3
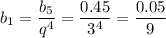
Сумма первых восьми членов этой прогрессии равна:

при