В решении.
Объяснение:
Сравнить:
1) 4,7*10^-6 и 5,9*10^-7;
4,7*10⁻⁶ и 5,9*10⁻⁷;
1/4,7⁶ и 1/5,9⁷;
1/4,7⁶ > 1/5,9⁷;
Чем больше знаменатель, тем меньше значение дроби.
2) 1,23*10^6 и 0,12*10^7;
1,23*10⁶ и 0,12*10⁷;
Привести второе число к стандартному виду:
1,23*10⁶ и 1,2*10⁶;
1,23*10⁶ > 1,2*10⁶;
Если показатели степени одинаковые, больше то число, основание которого больше.
3) 31,6*10^-8 и 0,061*10^-8;
31,6*10⁻⁸ и 0,061*10⁻⁸;
1/31,6⁸ и 1/0,061⁸;
Привести оба знаменателя к стандартному виду:
1/3,16⁹ и 1/6,1⁶;
1/3,16⁹ < 1/6,1⁶;
Чем больше знаменатель, тем меньше значение дроби.
Собственная скорость теплохода 12 км/ч.
Объяснение:
Задача:
Теплоход 35 км по течению реки и вернулся назад, израсходовав на обратный путь на 1 час больше. Чему равна собственная скорость теплохода, если скорость течения равна 2 км/ч?
Пусть х - собственная скорость теплохода, тогда
х + 2 - скорость теплохода по течению реки
х - 2 - скорость теплохода против течения реки
35 : (х + 2) - время в пути по течению реки
35 : (х - 2) - время в пути против течения реки
По условию
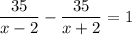
Решаем это уравнение
35(х + 2) - 35(х - 2) = х² - 4
35х + 70 - 35х + 70 = х² - 4
х² = 144
х = 12 (км/ч)
Получаем, что ∠1 + ∠2 + ∠3 + ∠4 = 180° + 180° = 360°. Пусть градусная мера второго угла х, тогда первого — х + 50. Составим уравнение:
х + х + 50 + х + х + 50 = 360, 4х + 100 = 360, 4х = 260, х = 65. Итак, ∠2 = 65°,∠4 = 65°, ∠1 = 115°, ∠3 = 115°.
ответ: 65°, 115°