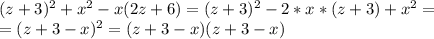
ответ: Нет.
Из условия следует, что f(x) = (x – a)(x – b), где a ≠ b.
Пусть искомый многочлен f(x) существует.
Тогда, очевидно f(f(x)) = (x – t1)²(x – t2)(x – t3).
Заметим, что t1, t2, t3 — корни уравнений f(x) = a и f(x) = b, при этом корни этих уравнений не совпадают, поэтому можно считать, что уравнение f(x) = a имеет один корень x = t1.
Рассмотрим уравнение f(f(f(x))) = 0. Его решения, очевидно, являются решениями уравнений f(f(x)) = a и f(f(x)) = b. Но уравнение f(f(x)) = a равносильно уравнению f(x) = t1 и имеет не более двух корней, а уравнение f(f(x)) = b — не более четырех корней (как уравнение четвертой степени).
То есть уравнение f(f(f(x))) = 0 имеет не более 6 корней.
х км/ч - скорость пешехода
у км/ч - скорость велосипедиста
50 мин + 10 мин = 60 мин = 1 час - время, за которое пешеход расстояние от поселка до места встречи.
10 мин = 1/6 часа - время, которое понадобилось велосипедисту , чтобы преодолеть это же расстояние от поселка до места встречи.
Первое уравнение:
1 · х = 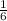 · у
· у
Умножим обе части на 6 и получим:
6x = y
полчаса = 0,5 часа
По условию 4x > 0,5y на 3 км.
Второе уравнение:
4x - 0,5y = 3
Во второе уравнение подставим у=6х и решим относительно х.
4х - 0,5·6х = 3
4х - 3х = 3
х = 3 км/ч - скорость пешехода
6 · 3 = 18 км/ч - скорость велосипедиста.
ответ: 3 км/ч;
18 км/ч