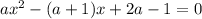
Нам дано уравнение вида ax² + bx + c = 0 (квадратное уравнение). Оно имеет 2 разных корня только в том случае, когда дискриминант (D = b² - 4ac) имеет значение больше нуля.
Попробуем рассчитать дискриминант данного уравнения:
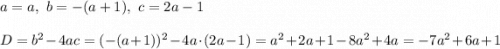
Выходит, что -7a^2 + 6a + 1 должно быть больше нуля:
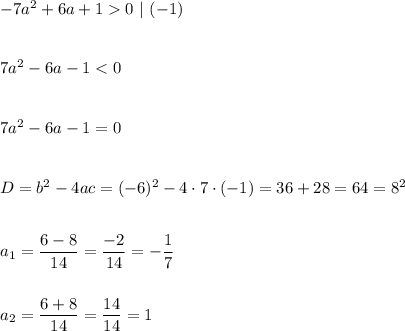
При a = 2, получим: 7 * 2^2 - 6 * 2 - 1 = 7 * 4 - 12 - 1 = 28 - 12 - 1 = 15 > 0, тогда методом интервалов:
++++++++++++++[-1/7]-------------------[1]+++++++++++++>
Так как у нас знак неравенства "<", то берём все отрицательные значения:
При a ∈ (- 1/7; 1) уравнение имеет два корня.
ответ: 14 дней.
Объяснение:
Решение.
Первоначальная производительность бригады равна х деталей в день.
Тогда 140 деталей она изготовит за 140/х дней.
Если изготавливать на 4 детали больше, то 140 деталей она изготовит за 140/(х+4) дня, что на 4 дня меньше запланированного. Тогда
140/x - 140/(x+4)=4;
140(x+4)-140x=4x(x+4);
140x+560-140x=4x²+16x;
4x²+16x-560=0; [:4]
x²+4x-140=0;
x1=10; x2= -14 - не соответствует условию.
х=10 деталей в день.
За 140 : 10= 14 дней бригада могла закончить работу первоначально
24 -(-1/22/ = 24+ 1/22 = 24 1/22