1) 10 км - 3000 шт.
2) 100 км - 116 шт.
Объяснение:
Тут тільки с калькулятором працювати і думати логічно. Тут логіка в 99% до знайти відповідь.
Але я знайшов алгоритм, як можна більш науково і точно розв'язати цю задачу:
1) Шукаємо суму суми і різниці річок:
3116+2884=6000(шт.)
2) Шукаємо середнє арифметичне:
6000:2=3000(шт.)
3) Тут вже можна використати два
а) Від суми річок відняти 3000: 3116-3000=116(шт.)
б) Від 3000 відняти різницю річок: 3000-2884=116(шт.)
Відповідь: 1) 10 км - 3000 шт. - це очевидно, оскільки ці річки перші згадуються в умові, а потім річки понад 100 км.
2) Понад 100 км - 116 шт.
Запишем систему уравнений в исходном виде:
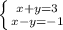
А) Подставим пару чисел (1;1):
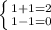
Отсюда делаем вывод, что пара чисел (1;1) не является решением данной системы уравнений, так как не удовлетворяет ни 1 уравнению системы.
Б) Подставим числа (1;2)
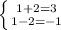
Отсюда делаем вывод, что пара чисел (1;2) является решением данной системы уравнений, так как удовлетворяет обоим уравнениям системы.
В) Подставим пару чисел (2;1):
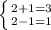
Отсюда делаем вывод, что пара чисел (2;1) не является решением данной системы уравнений, так как данная пара чисел не удовлетворяет второму уравнению.
Г) Подставим пару чисел (2;2):
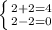
Отсюда делаем вывод, что пара чисел (2;2) не является решением данной системы уравнений, так как не удовлетворяет ни 1 уравнению системы.
Видео «Неопределенные системы линейных уравнений - метод решения, пример» посвящено вопросу о том, как решать неопределенные системы. Если рассматривать систему, состоящую из n уравнений с n неизвестными, т.е. системы, матрица коэффициентов которых - квадрат, то необходимым условием её решения методом Крамера или матричным методом является неравенство нулю её определителя. Т.е. если определитель матрицы равен нулю, то решить такую систему указанными методами нельзя. Но это совсем не означает, что эта система уравнений не имеет решения вообще. В этом случае возможны два варианта. Первый из них, это когда решений действительно нет, т.е. система несовместна. Во втором случае система имеет множество решений (неопределенная система). Именно для решения таких систем и предназначен метод, который будет рассмотрен в данном видео уроке. Здесь также будет решен пример, в котором требуется решить неопределенную систему линейных уравнений. Процесс решения системы сопровождается подробным объяснением. Видео урок «Неопределенные системы линейных уравнений - метод решения, пример» вы можете смотреть онлайн в любое время абсолютно бесплатно. Успехов!