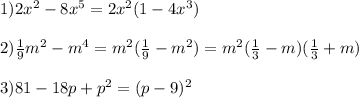
\[x_0=-\frac{b}{2a}=-\frac{0}{2\cdot \left(-1\right)}=0\]
Подставим найденную абсциссу в уравнение функции и найдем ее ординату:
\[y_0=-0^2+4=4\]
Итак, вершиной параболы будет точка (0; 4).
Далее нужно найти точки, которые принадлежат графику параболы. Сделать это легко. Берем несколько произвольных значений переменной х и вычисляем для них значение переменной у. Полученные пары чисел будут координатами искомых точек.
х = 1: y\left(1\right)=-1^2+4=3 —точка с координатами (1; 3).
х = 2: y\left(2\right)=-2^2+4=0 —точка с координатами (2; 0).
х = —1: y\left(-1\right)=-{\left(-1\right)}^2+4=3 —точка с координатами (—1; 3).
х = —2: y\left(-2\right)=-{\left(-2\right)}^2+4=0 —точка с координатами (—2; 0). Нанесем найденные точки на координатную плоскость и начертим график функции y = —x^2 + 4
(Рисуешь точку и проводишь линии в право ,влево ,вперед и назад.Расставляешь числа ,рисуешь дугу с самого низа до верха по второе число и спускаешься вниз)Думаю понятно объяснила.
1.
а) 3(a + 2) + b(a + 2) = (3 + b) * (a + 2)
б) 4f(5m-3n) - 5r(5m-3n) = (4f - 5r) * (5m - 3n)
в) 5m(a - 3d) + a - 3d = 5m(a - 3d) + 1(a - 3d) = (5m + 1) * (a - 3d)
г) 5m(a - 3d) - a + 3d = 5m(a - 3d) + 1(a - 3d) = (5m + 1) * (a - 3d)
2.
а) 3a +6 + ab + 2b = 3(a + 2) + b(a + 2) = (3 + b) * (a + 2)
б) 20fr - 12fn - 25rm + 15mn = 4f(5r - 3n) - 5m(5r -3n) = (4f - 5m) * (5r - 3n)
в) ab + ac + af + b + c + f = a(b + c + f) + 1(b + c + f) = (a + 1) * (b + c + f) (думаю, у Вас тут ошибка, и должна быть именно буква b)
г) x⁵ + x⁴ + x³ +x² + x + 1 = x⁵ + x⁴ + x³ +x² + x¹ + 1 = x³(x² + x¹ + 1) + 1(x² + x¹ + 1) = (x³ + 1) * (x² + x¹ + 1)