В решении.
Объяснение:
Постройте в одной и той же координатной плоскости графики
функций у=х² и у= -x+6 и найдите координаты точек пересечения этих графиков.
1) у = х² - график квадратичной функции, классическая парабола с вершиной (0; 0), ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить у:
Таблица:
х -4 -3 -2 -1 0 1 2 3 4
у 16 9 4 1 0 1 4 9 16
2) у= -x + 6 - график линейной функции, прямая линия. Для построения достаточно двух точек, для точности определим три.
Придать значения х, подставить в уравнение, вычислить у:
х -1 0 1
у 7 6 5
3) Согласно построения координаты точек пересечения:
(-3; 9); (2; 4).
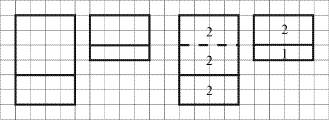
Нарисуем два луга, один больше другого вдвое.
Разделим большой луг на две части. Первая часть – это работа всей артели в первые полдня. Вторая часть – работа половины артели во вторую половину дня. Значит, первая часть большого луга вдвое больше второй.
Меньший луг тоже разделим на две части. Первая часть меньшего луга равна второй части большого луга, так как ее выкосила такая же группа косцов. Значит, первая часть меньшего луга равна 1/3 большого луга. 1/3 меньшего луга = 1/6 большого луга.
Вторую часть меньшего луга косил один косец целый день. Значит, большой луг один косец косил бы 6 дней. Значит, две трети большого луга один косец косил бы 4 дня. А так как вся артель косила две трети большого луга полдня, то артель состояла из 8 косцов.
ответ: 8 косцов.
-3х+6х=-4а+с
(-3+6)х=с-4а
3х=с-4а или х=(с-4а)÷3