y = - x³ + 3x² + 4
Найдём производную :
y' = (- x³)' + 3(x²)' + 4' = - 3x² + 6x
Приравняем производную к нулю , найдём критические точки :
- 3x² + 6x = 0
- 3x(x - 2) = 0
x₁ = 0
x - 2 = 0 ⇒ x₂ = 2
Обе критические точки принадлежат заданному отрезку. Найдём значения функции в критических точках и на концах отрезка и сравним их .
y(- 3) = -(- 3)³ + 3 * (- 3)² + 4 = 27 + 27 + 4 = 58
y( 3) = - 3³ + 3 * 3² + 4 = - 27 + 27 + 4 = 4
y( 0) = - 0³ + 3 * 0² + 4 = 4
y(2) = - 2³ + 3 * 2² + 4 = - 8 + 12 + 4 = 8
Наименьшее значение функции равно 4, а наибольшее равно 58 .
№6
3х – 5 (2х + 1) = 3 ( 3 – 2х)
3х–10х–5=9–6х
3х–10х+6х=9+5
–х=14
х=–14
ответ: –14
№5
х²–3х–3у–у²= –3(х+у)+х²–у²= –3(х+у)+(х+у)(х–у)= (х+у)(–3+х–у)
№1
(а +6)²–2а(3 – 2а)=а²+12а+36–6а+4а²= 5а²+6а+36
№2
Система:
5х – 2у = 11
4х – у = 4 |*(–2)
Система:
5х – 2у = 11 (Ур 1)
–8х+2у=–8 (Ур 2)
Сложим уравнения 1 и 2, получим:
–3х=3
х=–1
Подставим значение х у уравнение 1, получим:
5*(–1)–2у=11
–5–2у=11
–2у=16
у=–8
ответ: х=–1; у=–8
№4
Пусть х км– путь в третий день, тогда во второй х+5, а в первый (х+5)+10
Составим уравнение:
х+(х+5)+(х+5+10)=50
х+х+5+х+5+10=50
3х=50–10–5–5
3х=30
х=10
Тогда в третий день 10 км, во второй 10+5=15 км, в первый 10+5+10=25 км
ответ: Первый день 25 км; второй день 15 км; третий день 10 км.
№3
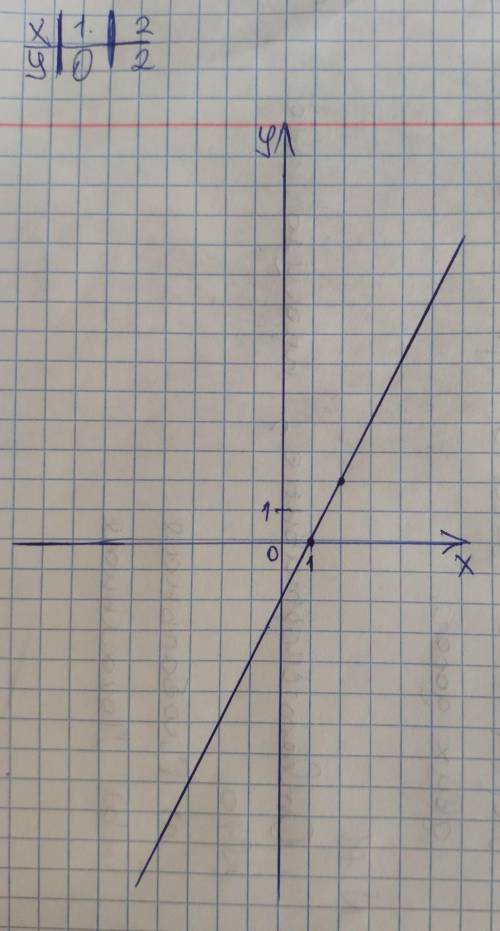
Кординаты точки А х=–10; у=–20.
Подставим значения в функцию у = 2х – 2, получим:
–20=2*(–10)–2
–20=–20–2
–20≠–22
Следовательно график НЕ проходит через точку А.
График во вложении
2х=17-7
х=10/2
х=5
график прямой проходит через точки
(0;-8)
(4;0)
(12х+18)1,4=0
16,8х+25,2=0
16,8х=-25,2
х=-1,5
Проверка:
(12*(-1,5)+18)1,4=(-18+18)1,4=0