1)
у=2х+1
у=2х-3
у=х+7
Эти линейные функции вида у=kx+b, где k-это угловой коэффициент, с его изменением будет меняться угол наклона прямой к оси Ох, значит, функции с одинаковыми угловыми коэффициентами будут параллельны друг другу. Отсюда параллельные функции:
у=2х+1 и у=2х-3. Эти графики функций можно построить по двум точкам каждый. Находим точки:
у=2х+1
х=0
у=2*0+1=0+1=1
(0;1)
х=1
у=2*1+1=3
(1;3)
у=2х-3
х=0
у=2*0-3
у=-3
(0;-3)
х=1
у=2*1-3=-1
(1;-1)
у=х+7
х=0
у=7
(0;7)
х=2
у=2+7=9
(2;9)
По этим точкам строим графики.
2)
Поскольку графики прямые, два из которых параллельны, то эти 2 графика будут пересекать третий, т.е. у=2х+1 и у=2х-3 будут пересекать график у=х+3, а график у=х+7 пересекать его не будет, т.к. он с тем же угловым коэффициентом.
Для нахождения координат пересечения приравняем функции:
2х+1=х+3
2х-х=3-1
х=2
у=2+3=5
координата пересечения (2;5)
2х-3=х+3
2х-х=3+3
х=6
у=6+3=9
(6;9)
Объяснение:
;
;
и будет искомой фигурой.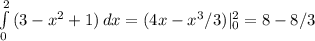
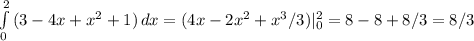
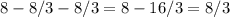(кв. ед.)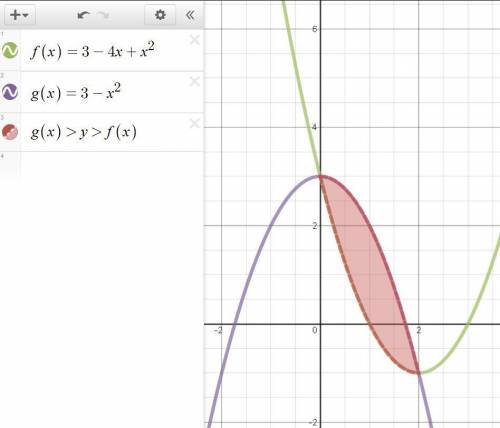
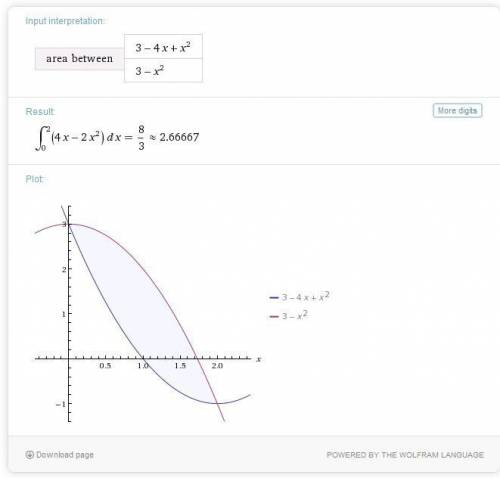
x=3-1 2/7
x=1 5/7
1 2/9-x=1/3
-x=1/3-1 2/9
-x=3/9-11/9
-x=-8/9
x=8/9