1.
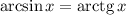
ОДЗ: арксинус определен при ![x\in[-1;\ 1]](/tpl/images/1421/5878/61ea0.png)
Найдем синус левой и правой части:
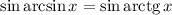
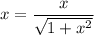
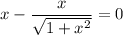
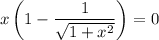
Уравнение распадается на два. Для первого уравнения получим:
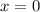
Решаем второе уравнение:
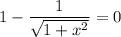
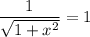
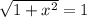
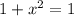
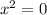
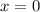
Таким образом, уравнение имеет единственный корень 0.
ответ: 0
2.
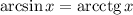
ОДЗ: арксинус определен при
Найдем синус левой и правой части:
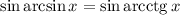
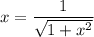
Так как в правой части стоит положительная величина, то и левая часть должна быть положительной, то есть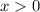 
.
Возведем в квадрат обе части:
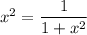
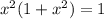
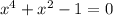
Решим биквадратное уравнение:
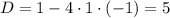
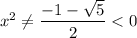
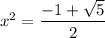
Находим х:
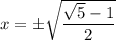
Однако, так как было выявлено ограничение 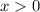, то отрицательный корень не попадает в ответ.
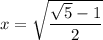
Оценив значение полученного корня, мы понимаем, что он удовлетворяет исходной ОДЗ:
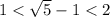
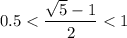
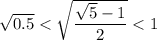
ответ: 
Чтобы выяснить,какая из точек не принадлежит графику достаточно координаты этих точек подставить в функцию,которой задан график.
Если получится верное равенство,то точка принадлежит графику, а если неверное, то не принадлежит.
Данная функция прямая, параллельная оси ОХ, вида
у=k*х+b
k=0
k – угловой коэффициент , b – свободный член(-5) , x – независимая переменная.
у=0*х-5
НО
Мы видим , что данная функция не зависит от Х, при любом его значении у=-5 , то есть можно без расчетов найти точку,которая не принадлежит графику. Это точка 3, потому что у=0,а не -5.
Если мы этого не видим,то подставляем:
1) (0: -5)
-5=0*0-5
-5=-5 - принадлежит
2) (-5:-5)
-5=0*-5-5
-5=-5 - принадлежит
3) (-5: 0 )
0=0*-5-5
0≠-5 - не принадлежит
4) (5: -5 )
-5=0*5-5
-5=-5 - принадлежит
