В решении.
Объяснение:
1.
5•5⁵ = 5¹⁺⁵ = 5⁶ = 3125;
(3b)*(3b)⁶ = (3b)¹⁺⁶= (3b)⁷ = 3⁷*b⁷ = 2187b⁷;
(-1,2)³•(-1,2)⁴ = (-1,2)³⁺⁴ = (-1,2)⁷ = -3,5831808;
(-6)³•(-6)²•(-6)⁷ = (-6)³⁺²⁺⁷ = (-6)¹² = 2 176 782 336;
b⁶b⁸b = b⁶⁺⁸⁺¹ = b¹⁵;
(n+m)¹⁵(n+m)⁵ = (n+m)¹⁵⁺⁵ = (n+m)²⁰;
2. Запишите в виде степени с основанием 2:
128 = 2⁷;
1024 = 2¹⁰;
16•2⁵ = 2⁴*2⁵ = 2⁴⁺⁵ = 2⁹;
3. Запишите в виде степени с основанием 3:
81 = 3⁴;
3⁶•3 = 3⁶⁺¹ = 3⁷;
81•3² = 3⁴*3² = 3⁶;
27•3 = 3³*3 = 3⁴;
4.
10¹²:10⁴ = 10¹²⁻⁴ = 10⁸ = 100 000 000;
d²⁴:d¹² = d²⁴⁻¹² = d¹²;
(m+n)¹⁰:(m+n)⁵ = (m+n)¹⁰⁻⁵ = (m+n)⁵;
5. Запишите в виде степени с основанием 2:
32:2 = 2⁵:2 = 2⁵⁻¹ = 2⁴
2¹⁰:2 = 2¹⁰⁻¹ = 2⁹;
6. Запишите в виде степени с основанием 3:
27:3² = 3³:3² = 3³⁻² = 3¹ = 3;
3⁸:3⁴ = 3⁸⁻⁴ = 3⁴;
5⁸•5⁷/5⁴•5⁹ = 5⁸⁺⁷/5⁴⁺⁹ = 5¹⁵/5¹³ = 5²;
3⁶•3³/3⁵•3•3 = 3⁶⁺³/3⁵⁺¹⁺¹ = 3⁹/3⁷ = 3²;
3⁶•2⁷/6⁵ = (3⁶*2⁶*2)/6⁵ = (6⁶*2)/6⁵ = 6⁶⁻⁵*2 = 6*2 = 12;
а⁵(а²)⁸ = а⁵*а²*⁸ = а⁵*а¹⁶ = а⁵⁺¹⁶ = а²¹;
а⁵(а³)⁴(а²)³ = а⁵*а³*⁴ *а²*³ = а⁵*а¹²*а⁶ = а⁵⁺¹²⁺⁶ = а²³;
а⁸(а⁴)⁴/(а³)⁴ = а⁸*а⁴*⁴/а³*⁴ = а⁸*а¹⁶/а¹² = а²⁴/а¹² = а²⁴⁻¹² = а¹².
По определению, 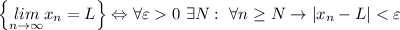
Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение 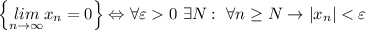
2) 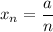
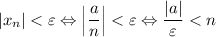
А значит, если взять ![N=\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/0d89e.png) (*),
(*),  . И правда:
. И правда: 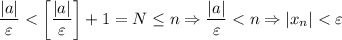
(*) Очевидно, что для любого допустимого значения  выражение
выражение ![\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/ae843.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
А это и означает, что предел данной последовательности равен 0
4) 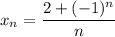

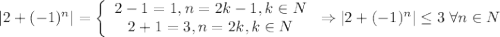
А значит, если взять ![N=\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/a4ca4.png) (**),
(**),  . И правда:
. И правда: ![\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|](/tpl/images/3820/0626/49458.png)
(**) Очевидно, что для любого допустимого значения  выражение
выражение ![\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/698f8.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
А это и означает, что предел данной последовательности равен 0
___________________________
2) a=1. Тогда 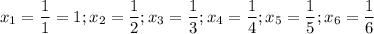
4)

___________________________
Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x. 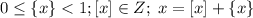

а2 + б2 = 58