Объяснение:
Так как плоскость KCNM перпендикулярна к ребру АЕ, то стороны МК и МN, а также диагональ СМ сечения KCNM перпендикулярны к АЕ. Так как диагональ СМ лежит в плоскости равнобедренного треугольника AЕС, то она пересекает прямую EO, являющуюся высотой этого треугольника. С другой стороны, диагональ KN, лежащая в плоскости треугольника BED (и, как сейчас будет доказано, параллельная основанию BD этого треугольника), тоже пересекает прямую ЕО, являющуюся высотой треугольника BED. А так как плоскость KCNM имеет с прямой ОЕ только одну общую точку О1, то в этой точке диагонали KN и МС пересекаются друг с другом.
Плоскость KCNM перпендикулярна к ребру АЕ; потому углы ЕМК и EMN - прямые. Прямоугольные треугольники ЕМК и EMN равны (доказать!); следовательно, MK=MN и EK=ЕN. Из последнего равенства вытекает, что KN||BD и что KО1 = О1N. Следовательно, диагонали МС и KN взаимно перпендикулярны и, значит, Scеч. = 1/2МС • KN.
Диагональ МС находим из прямоугольного треугольника АМС, где
∠ CAM = φ и AC = a√2 . Получаем МС = a√2 sin φ.
Диагональ KN находим из равнобедренного треугольника KEN, где ∠ EKN = φ. Имеем КN = 2 • О1E • ctg φ, где О1E = ОЕ - ОО1 . Отрезок ОЕ определяется из треугольника АОЕ (или ВОЕ); находим . Отрезок же OO1 определяется из треугольника ОСО1 , где ∠ OCO1 = 90°- ^MAС = 90° - φ.
3. 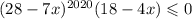
Заметим, что так как 2020 - четное число, то 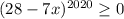 (число в четной степени всегда
(число в четной степени всегда 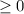 ). Поэтому первый множитель на знак левой части влиять не будет и его можно опустить. При этом стоит учесть, так это то, что если
). Поэтому первый множитель на знак левой части влиять не будет и его можно опустить. При этом стоит учесть, так это то, что если 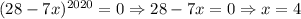 , то имеем :
, то имеем : 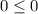 , а это верно. Поэтому нужно запомнить , что x = 4 - решение.
, а это верно. Поэтому нужно запомнить , что x = 4 - решение.
Если 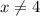 , то первый множитель положителен и на него можно поделить обе части, сохранив знак. Итого:
, то первый множитель положителен и на него можно поделить обе части, сохранив знак. Итого:
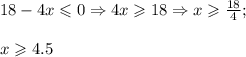
Решение неравенства - x = 4 и все 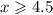 . Наименьшие целые решения - 4, 5 и 6. Их произведение равно 120.
. Наименьшие целые решения - 4, 5 и 6. Их произведение равно 120.
ОТВЕТ: 1) 120.
4. Область определения - все числа, которые можно подставить вместо x.
Под каждым из корней должно быть неотрицательное число, а знаменатель дроби должен быть отличен от 0. Область определения - все числа, удовлетворяющие системе из четырех неравенств 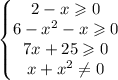 .
.
Из первого неравенства следует, что 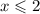 .
.
Решим второе неравенство: оно равносильно неравенству 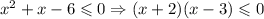 . Решением данного неравенство является отрезок [-2; 3].
. Решением данного неравенство является отрезок [-2; 3].
Третье неравенство: 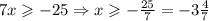 .
.
Четвертое: 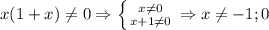
Так как у нас была система, ищем пересечение множеств решений всех 4 неравенств: ![x\in[-3;-1)\cup(-1;0)\cup(0;2].](/tpl/images/1359/4742/04668.png)
Все целые числа, принадлежащие области определения: -3; -2; 1; 2 (-1 и 0 выпадают, т.к. скобки круглые). Их сумма равна -2.
ОТВЕТ: 2) -2
ответ : 4,4