1)
![|2x-5|\leq 3\\\\\left \{ {{2x-5\leq3 } \atop {2x-5\geq-3}} \right.\\\\\left \{ {{2x\leq8 } \atop {2x\geq2 }} \right. \\\\\left \{ {{x\leq4 } \atop {x\geq1 }} \right.\\\\Otvet:\boxed{x\in[1;4]}](/tpl/images/0672/9676/83574.png)
2)
x² - 2x - 8 ≥ 0
(x - 4)(x + 2) ≥ 0
+ - +
__________[- 2]__________[4]__________
//////////////////////// ///////////////////////
Otvet : x ∈ (- ∞ ; - 2] ∪ [4 ; + ∞)
3)
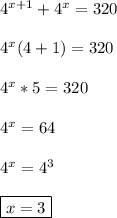
см. рисунок
1) А
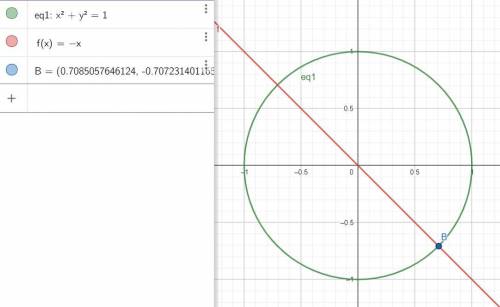
2) В
3) С
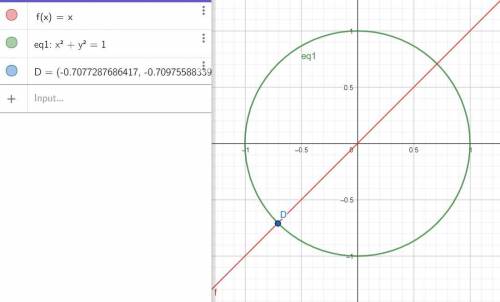
4) D
Объяснение:
а) 2пи - полный оборот, поэтому все точки будут слиты в одну. 6 пи, 8 пи кратны 2 пи поэтому там то же самое. вывод: достаточно построить 1 точку в каждом случае
б) пи на четыре = 45 градусов. табличное значение.
в) пи на три = 60 градусов. табличное значение
г) при единичном круге х = косинус угла поворота у = синус угла поворота
д) реально строить хорошо - прочертить круг и пересекать его лучом соответствующего угла отклонения. Для 1) и 2) и 4)
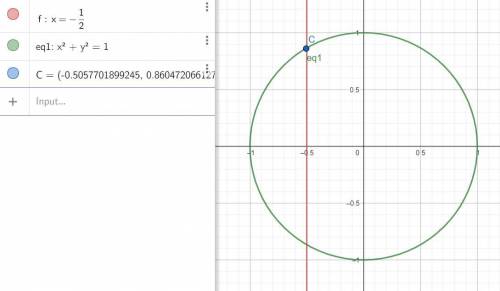
Для 3) 2 пи на три = 120 градусов, т.е. 90 + 30, у єтих точек абсциса (х) будет = 1/2 по табличному значению синуса - посему - линия по этой абсцисе - и точка пересечения с кругом - искомая.
потянет на лучший ответ?
Объяснение: -3≤2x-5≤3 2≤2x≤8 1≤x≤4
метод интервалов (x-4)(x+2)≥0 x∈(-∞;-2]∪[4;+∞)
5*4^x=320 4^x=64 x=3