1) -41/30
2) 2(x-0.5)
3) 2(x-3.5)(x-2)
4) x= - 1.75
Объяснение:
1) 1.3+1.6*(1 2/3 /2.5 -2) = 1.3+1.6*(5/3 * 2/5 -2) = 1.3 + 1.6*(2/3 - 2) =
=1.3 + 8/5 *(2/3 - 6/3) = 1.3 + 8/5*(-4/3)= 13/10 - 40/15 = 39/30 - 80/30 = - 41/30
2) (2x2 + 7x -4)/(x+4) =
x1,2= (-7+-корень(49+4*2*4))/2*2=(-7+-корень(81))/4= (-7+-9)/4
x1=(-7+9)/4=0.5
x2=(-7-9)/4= - 4
раскладываем на множители
(2x2 + 7x -4)/(x+4) = 2(x-0.5)*(x+4)/(x+4) = 2*(x-0.5)
3) (x - 2)(x + 2) - 3x + (4-x)^2 + 2 = x^2 - 4 - 3x + 16 - 8x + x^2 +2 =
=2x^2 - 11x + 14
ищем корни
x1,2= (11+-корень(121-4*2*14))/4=(11+- 3)/4
x1 = 3.5
x2 = 2
ответ 2(x-3.5)(x-2)
4) x^2 - 9 = x^2 + 4x - 2
4x=-7
x= - 1.75
Множества равны, если они состоят из одних и тех же элементов.
1.
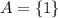 - множество, элементом которого является число 1
- множество, элементом которого является число 1
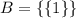 - множество, элементом которого является множество {1}, элементом которого является число 1 (так называемая, система множеств)
- множество, элементом которого является множество {1}, элементом которого является число 1 (так называемая, система множеств)
Множества не равны, так как элементы множеств имеют даже разные типы: элемент множества А - число, элемент множества В - множество.
2.
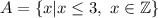 - множество, элементами которого являются все целые числа, не большие 3. Это числа 3, 2, 1, 0, -1, -2 и так далее в порядке убывания.
- множество, элементами которого являются все целые числа, не большие 3. Это числа 3, 2, 1, 0, -1, -2 и так далее в порядке убывания.
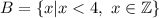 - множество, элементами которого являются все целые числа, меньшие 4. Это числа 3, 2, 1, 0, -1, -2 и так далее в порядке убывания.
- множество, элементами которого являются все целые числа, меньшие 4. Это числа 3, 2, 1, 0, -1, -2 и так далее в порядке убывания.
Эти множества равны.
3.
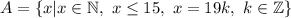 - множество состоит из натуральных чисел, не больших 15, которые делятся на 19. Но среди первых 15 натуральных чисел нет таких, которые делились бы на 19. Значит, это пустое множество.
- множество состоит из натуральных чисел, не больших 15, которые делятся на 19. Но среди первых 15 натуральных чисел нет таких, которые делились бы на 19. Значит, это пустое множество.
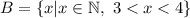 - множество состоит из натуральных чисел, которые больше 3, но меньше 4. Но таких натуральных чисел не существует. Значит, это тоже пустое множество.
- множество состоит из натуральных чисел, которые больше 3, но меньше 4. Но таких натуральных чисел не существует. Значит, это тоже пустое множество.
Эти множества равны.
4(a+2)²-4(4a+5)=4a²+16a+16-16a-20=4a²-4=4(a-1)(a+1)>0
a<-1 U a>1
2)x1*x2<0
4a+5<0
4a<-5
a<-1,25
a∈(-∞;-1,25)