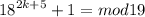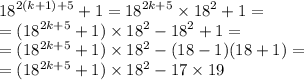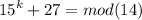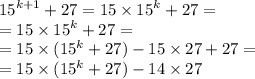1) а) a^2*b + a*b^2 = ab*(a+b) = 4*5 = 20
б) a^2 + b^2 = a^2 + 2ab + b^2 - 2ab = (a+b)^2 - 2ab = 5^2 - 2*4 = 17
2) а) 9^n - 2*3^n - 3 = 0
(3^n - 3)(3^n + 1) = 0
3^n + 1 > 0 при любом n.
3^n = 3
n = 1
б) 25^n - 2*5^n - 25 = 0
25^n - 2*5^n + 1 - 26 = 0
(5^n - 1)^2 - 26 = 0
(5^n - 1 - √26)(5^n - 1 + √26) = 0
5^n - 1 + √26 > 0 при любом n.
5^n = 1 + √26
n = log5 (1 + √26)
Если вы не поняли этого решения, значит, в задаче опечатка.
3) а) 6^31+6^30*5+6^29*5^2+ ... +6*5^30+5^31+5^32 =
= (6^32 - 5^32) / (6 - 5) + 5^32 = 6^32 - 5^32 + 5^32 = 6^32
б) 5^20+5^19*4+5^18*4^2+ ... +5*4^19+4^20-5^21 =
= (5^21 - 4^21) / (5 - 4) - 5^21 = 5^21 - 4^21 - 5^21 = -4^21