40 - первое число.
24 - второе число.
Объяснение:
Різниця двох чисел дорівнює 16, а 20% зменшуваного на 2 більше, ніж 25% від'ємника. Знайдіть ці числа.
Составляем систему уравнений согласно условия задания:
х - первое число.
у - второе число.
х-у=16
0,2х-0,25у=2
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х=16+у
0,2(16+у)-0,25у=2
3,2+0,2у-0,25у=2
-0,05у=2-3,2
-0,05у= -1,2
у= -1,2/-0,05
у=24 - второе число.
Теперь вычислить х:
х=16+у
х=16+24
х=40 - первое число.
Проверка:
40-24=16
0,2*40-0,25*24=8-6=2, верно.
Объяснение:
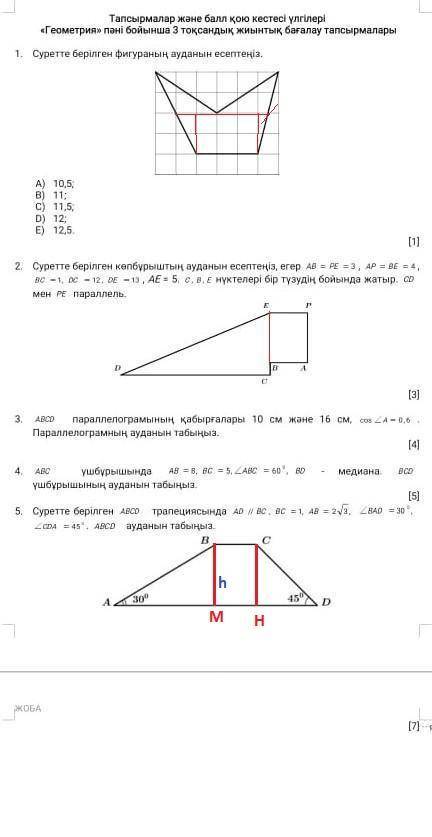
1 Sфиг = S1 + s2 + s3 + s4 + s 5 = 6 + 1 + 1/2( 3*2 - 2*1) + 1/2(3*2)= 10+5/2 = 12.5
2 Sавсдкр = 1/2(DC * CE) +(EB * AB ) = 1/2( 12 * 5) +( 4 * 3) = 30 +12 = 42
CE = √(13^2 - 12^2) = 
BE = CE - BC = 5 - 1 = 4
AB = PE = √(AE^2 - EB^2) = √(5^2 -4^2) = √(5+4)(5-4) =√9 =3
Sавсдкр = 1/2( 12 * 5) +( 4 * 3) = 30 +12 = 42
3 Sпараллелограмма= а * в * Sin a
Sin^2 a + Cos^ a = 1
Sin a = √(1 - cos^2 a) = √(1 - 0.6^2) = √0.64 = 0.8
Sавсд = 10*16*0.8 = посчитаешь
4
5. дано ВС = 1, АВ = 2√3, ∠А = 30, ∠Д = 45
Sавсд = ?
решение : Sавсд = 1/2* (АД + ВС ) * h
Из ΔАВМ, АВ - гипотенуза, катет BM = h = 0,5*АВ = √3 (против ∡=30 )
АМ = √ (АВ^2 - h^2)= √[(2√3)^2 - (√3)^2] = √4 =2
из ΔСДН , СН = ДН = √3 ( Δ прямоугольный и равнобедренный ∠с=∠д =45)
АД = АМ + МН + НД = 2+1 +√3 = 3 + √3
Sавсд = 1/2*( 1 + 3 + √3) * √3 = √3/2( 4 + √3) = 2√3 + 1.5