Целые числа называются взаимно простыми, если они не имеют никаких общих делителей, кроме ±1. Примеры: 14 и 25 взаимно просты, а 15 и 25 не взаимно просты (у них имеется общий делитель 5).
Наглядное представление: если на плоскости построить «лес», установив на точки с целыми координатами «деревья» нулевой толщины, то из начала координат видны только деревья, координаты которых взаимно просты.
8, 15 — не простые, но взаимно простые.
6, 8, 9 — взаимно простые числа, но не попарно взаимно простые.
8, 15, 49 — попарно взаимно простые.
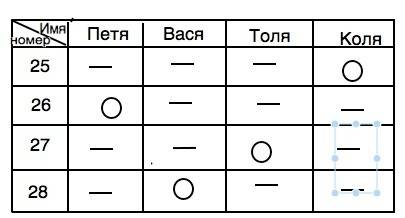
Составим таблицу ( см. рисунок).
1)Квартира Васи не 25 ( ее номер больше номера Пети) Ставим прочерк в столбике Васи в строке 25.
Номер квартиры Пети не самый большой - ставим прочерк в №28 столбика Пети
2) Квартира Толи не 25 ( ее номер больше номера Коли) и не 28 ( она между квартирами Пети и Васи) Ставим прочерк в столбике Толи в строке 25 и 28.
Квартира Коли не № 28 (т.к. номер квартиры Толи больше)- ставим прочерк в строке 28 столбика Коли.
3) № 28 остался свободным для Васи. Ставим кружок ( или галочку). Исключаем остальные номера из его столбика.
Тогда № квартиры Толи на 1 меньше Васиной - 27, а Пети на 1 меньше Толиной, это 26.
Получили: Квартира 26 у Пети, а 27 у Толи.
х^2 - 4 = (4х - 4)(х+1)
х^2 - 4 = 4х^2 - 4
х^2 = 4х^2
х^2 - 4х^2 = 0
-3х^2 = 0
х = 0
4(х+2)(х-3) = (х-2)(х+2)
(4х+8)(х-3) = х^2 - 4
4х^2 - 4х - 24 = х^2 - 4
4х^2 - 4х - 24 - х^2 + 4 = 0
4х^2 - 4х - х^2 - 20 = 0
3х^2 - 4х - 20 = 0
3х^2 - 4х = 20
х € (-2 ; 3 1/3)