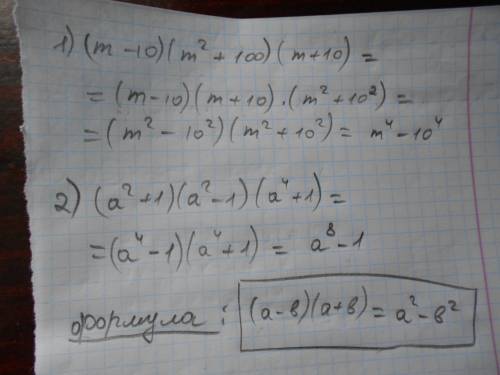
См. Объяснение
Объяснение:
Задание 1.
Докажем, что при каждом целом k значение (k+5) (k²-k+1)-k (k+2)² +3 делится на 8.
Раскроем скобки и приведём подобные члены:
(k+5) (k²-k+1)-k (k+2)² +3 = k³-k²+k+5k²-5k+5-k³-4k²-4k+3 = 8-8k = 8· (1-k)
В результате, после раскрытия скобок и приведения подобных, мы получили произведение, в котором один из сомножителей делится на 8. Значит, и всё произведение делится на 8.
Что и требовалось доказать.
Задание 2.
Первое выражение:
х = 49p² - q² - это разность квадратов двух чисел, которая равна произведению суммы и разности оснований:
х = 49p² - q² = (7p + q) · (7p -q).
Второе выражение:
у = 8х⁵ - 4х³ - можно преобразовать в произведение, если вынести за скобки 4х³ (это первый ):
у = 8х⁵ - 4х³ = 4х³ · (2х² - 1);
у = 8х⁵ - 4х³ - можно преобразовать в произведение, если вынести за скобки 8х³ (это второй ):
у = 8х⁵ - 4х³ = 8х³ · (х² - 1/2) = 8х³· (х + 1/√2) · (х - 1/√2);
в этом случае мы представили (х² - 1/2) как разность квадратов двух чисел.
Объяснение:
(2а+5в) + (8а – 11в) + (9в – 5а) = 2а + 5в + 8а – 11в + 9в – 5а = 5а + 3в
(3х + 10у) – (6х + 3у) + (6у – 8х) = 3х + 10у – 6х – 3у + 6у – 8х = – 11х + 13у
(8с2 + 3с) + (-7с2 – 11с + 3) – (-3с2 – 4) = 8с2 + 3с – 7с2 – 11с + 3 +3с2 + 4 = 4с2 – 4с + 7
(2р2 + 3рс + 8с2) – (6р2 – рс – 8с2) = 2р2 + 3рс + 8с2 – 6р2 + рс + 8с2 = – 4р2 + 4рс + 16с2
10х2 – (7ах – 5х2 + 8а2) + (6ах – 4а2) = 10х2 – 7ах + 5х2 – 8а2 + 6ах – 4а2 = 15х2 – ах – 12а2
(3а + 5в) + (9а – 7в) + (-5а + 16в) = 3а + 5в + 9а – 7в – 5а + 16в = 7а + 14в
(2х – 11у) – (5х + 12у) + (3х – 17у) = 2х – 11у – 5х — 12у + 3х – 17у = – 40у
(3в2 + 2в) + (2в2 – 3в – 4) – (-в2 + 19) = 3в2 + 2в + 2в2 – 3в – 4 + в2 – 19 = 6в2 – в – 23
(8х2 + 2рх – 3р2) – (2х2 + 3рх – 3р2) = 8х2 + 2рх – 3р2 – 2х2 – 3рх + 3р2 = 6х2 – рх
5ру – (4р2 + 3у2 – 7ру) – (12ру – 3у2) = 5ру – 4р2 – 3у2 + 7ру – 12ру + 3у2 = 4р2