Очевидно, что первым взвешиванием нужно положить на обе чаши весов по одной любой монете.
После первого взвешивания возможны 2 варианта:
1). Весы находятся в равновесии. - Откладывем обе монеты в сторону, считая их настоящими.
Повторяем взвешивание двух из трех оставшихся монет. Равновесия в этом случае не будет, так как из трех монет только одна настоящая.
Таким образом, после второго взвешивания получаем неравновесное положение весов. Запоминаем положение стрелки весов и меняем ту монету, которая легче, на последнюю оставшуюся.
Если стрелка весов уйдет в больший перевес, то на весах находятся обе фальшивые монеты.
Если в меньший перевес, то та монета, которую сняли с весов после второго взвешивания, - фальшивая с недовесом, а на более тяжелой чаше весов - фальшивая с перевесом.
Если чаша, на которой поменяли монету, перевесила, то на ней - фальшивая с перевесом, а та, которую сняли, - фальшивая с недовесом.
2). Весы не в равновесии. Запоминаем положение стрелки весов и меняем ту монету, которая легче, на одну из трех оставшихся.
Во втором взвешивании возможны 3 варианта положения весов:
Если весы пришли в равновесие, то на них обе монеты настоящие, а та, которую сняли, - фальшивая с недовесом. Оставшиеся 2 монеты - настоящая и фальшивая с перевесом, - определяются третьим взвешиванием.
Если весы ушли в больший перевес, то на весах находятся обе фальшивые монеты.
Если чаша, на которой поменяли монету, перевесила, то на ней - фальшивая с перевесом, а та, которую сняли, - фальшивая с недовесом.
ответ: Запись в виде интервала: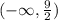 
Нотация построения множества: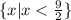 
Объяснение: Положим аргумент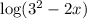 
больше 0, чтобы выяснить, где определено данное выражение.
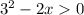
Решим относительно x.
Возведем 3 в степень 2.
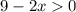
Вычтем 9 из обеих частей неравенства.
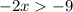
Разделим каждый член на -2 и упростим.
Разделим каждый член в выражении 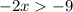на -2. При умножении или делении обеих частей неравенства на отрицательное значение, знак неравенства меняется на противоположный.
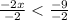
Сократим общий множитель -2.
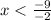
Деление двух отрицательных значений дает положительный результат.
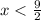
Решение включает все истинные интервалы.
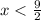
Областью определения являются все значения x, которые делают выражение определенным.
Запись в виде интервала: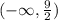
Нотация построения множества: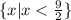
-1/(х+4) = 8/3
-1•3 = 8 • (х+4)
-3 = 8х + 32
8х = -3 - 32
8х = -35
х = -35/8
х = - 4,375
Проверка:
-1/(-4,375+4) =
- 1/(-0,375)=8/3 = 2 2/3