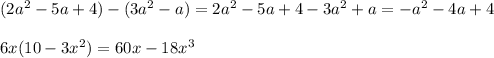
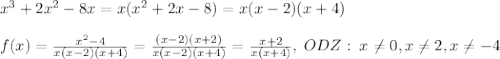
![lim_{x\to 0}\frac{x+2}{x(x+4)}=[\frac{2}{0}]=\infty \\\lim_{x\to -4}\frac{x+2}{x(x+4)}=[\frac{-2}{0}]=\infty](/tpl/images/0196/5667/7c566.png)
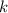. Перед этим учтем, что прямая проходит через начало координат - точку (0;0) (это очевидно, т.к. если 
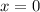, то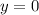 
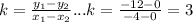
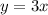. Любые прямые с тем же коэффициентом наклона будут параллельны данной прямой. В частности, например, 
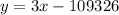параллельна исходной.
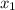будет абсциссой любой из точек на искомой прямой, а 
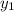- ординатой. Но не 
!
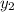