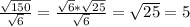
это не кубическая парабола.
------------------------------------------------------
Дано функция f(x) = x;
Если функция четная, то f(-x) = x.
Если не четная, то f(-x) = -x.
------------------------------------------------------
Рассмотрим эту ф-цию:
f(x) = y=x^5-x^3+x;
Найдем значение в точке -х:
f(-x) = (-x)^5 -(-x)^3 + (-x)
Так, как в нас степень нечетная, то:
f(-x) = (-x)^5 -(-x)^3 + (-x) = -x^5 + x^3 - x;
вынесем минус:
f(-x) = -(x^5 - x^3 + x);
Итак, мы имеем, что : f(-x) = -x, значит ф-ия f(x) - нечетная.
------------------------------------------------------------------------------------------------
Найдем найменшее значений ф-кции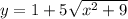 
Так, как в нас есть квадратный корень(а он всегда больше или равен нулю), то
найменшее значение y будет тогда, когда мы найдем найменшее значение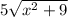 
: 
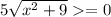
Поднесем к квадрату:
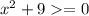. Мы можем найти найменшее значение вот этого неравенства. Это будет при х = 0 :) Тогда найдем найменшее значение у:
у = 1 + 5*3 = 1 + 15 = 16.
Наверное, всё-таки на обратную дорогу он потратил на 5 минут больше
1 ч. 5 мин.=13/12 ч.
Пусть х км/ч - скорость на подъёме, тогда скорость на спуске - (х+2) км/ч. Пусть у км - расстояние от станции до вершины горы, тогда расстояние от вершины горы до озера - (5-у) км. На дорогу от станции до озера рыболов затратил y/x+(5-y)/(x+2) или 1 час; на обратную дорогу - (5-у)/х + у/(х+2) или 1,1 часа. Составим и решим систему уравнений:
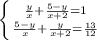
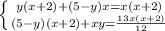
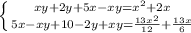
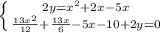
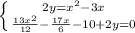
Произведём подстановку:
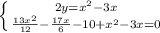
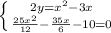
Домножим второе уравнение на 12/25:
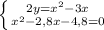
По теореме Виета корнями уравнения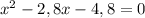 
являются 4 и -1,2. Так как скорость не может быть отрицательным числом, получаем, что скорость на подъёме была равна 4 км/ч, а на спуске 4+2=6 км/ч.
Путь от станции до вершины (4^2-3*4)/2=2 км, от вершины до озера 5-2=3 км.
ответ: скорость на подъёме 4 км/ч, скорость на спуске 6 км/ч.
