a) x-8≥2(x+½)+7
x-8≥2x+1+7
x-8≥2x+8
x-2x≥8+8
-x≥16
x≤-16
b) x(x+3)>(x+1)(x+3)
x²+3x>x²+4x+3
x²+3x-x²-4x>3
-x>3
x<-3
c) (3x-1)/5-(x+1)/2<1-x/7
2(3x-1)/10-5(x+1)/10<1-x/7
(6x-2-5x-5)/10<7/7-x/7
(x-7)/10<(7-x)/7
(70*(x-7))/10<(70*(7-x))/7
7*(x-7)<10*(7-x)
7x-49<70-10x
7x+10x<70+49
17x<119
x<119/17
x<7
d) (9x+2)/10-(10x-2)/9>2
(9*(9x+2)-10*(10x-2))/90>2
(81x+18-100x+20)/90>2
(-19x+38)/90>2
(90*(-19x+38))/90>2*90
-19x+38>180
-19x>180-38
-19x>-142
x<-142/19
x<-7 9/19
340 м
Объяснение:
Как я понял, самая короткая дорога, соединяющая противоположные выходы - это диагональ прямоугольника.
Обозначим стороны a и b = 140+a. По теореме Пифагора
a^2 + b^2 = 260^2
a^2 + (140+a)^2 = 260^2
a^2 + a^2 + 280a + 140^2 - 260^2 = 0
2a^2 + 280a + 19600 - 67600 = 0
2a^2 + 280a - 48000 = 0 | делим на 2
a^2 + 140a - 24000 = 0
D/4 = (b/2)^2 - ac = 70^2 + 24000 = 4900 + 24000 = 28900 = 170^2
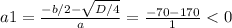 - не подходит
- не подходит
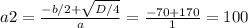
Значит, сторона а = 100 м, а сторона b = 100+140 = 240 м
В сумме получается 100 + 240 = 340 м
7, 3, 7, 0, 5, 8, 7, 4, 7, 17
Объяснение:
Натуральные числа - целые положительные числа, поэтому наименьшее натуральное число равен 1. По правилу счёта, количество целых чисел в замкнутом промежутке [A; B], где A и B целые числа определяется по формуле: B-A+1. Для решение задачи поступаем следующим образом:
1) если необходимо, для заданных промежутков определяем наибольшее подмножество в виде замкнутого промежутка, в котором содержаться двузначные натуральные числа;
2) посчитаем количество целых чисел, содержащихся в этом замкнутом промежутке.
[11; 17] ⇒ (17-11)+1=7
[0; 12] ⊃ [10; 12] ⇒ (12-10)+1=3
(-∞; 16] ⊃ [10; 16] ⇒ (16-10)+1=7
[0; 10) - нет таких чисел, 0
(-∞; 14) ⊃ [10; 14] ⇒ (14-10)+1=5
(92; +∞) ⊃ [92; 99] ⇒ (99-92)+1=8
[12; 19) ⊃ [12; 18] ⇒ (18-12)+1=7
(0; 13] ⊃ [10; 13] ⇒ (13-10)+1=4
(13; 20] ⊃ [14; 20] ⇒ (20-14)+1=7
(-∞; 26] ⊃ [10; 26] ⇒ (26-10)+1=17
7, 3, 7, 0, 5, 8, 7, 4, 7, 17