Объяснение:
а) 8/17 и 11/21
1) приведём дроби к НОЗ:
21 = 3 * 7
17 = 17
НОК (17; 21) = 3 * 7 * 17 = 357
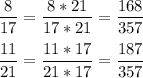
2) сравним дроби:
правило: из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше
Т.к. 187 > 168, значит:
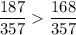 т.е.
т.е. 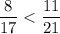
б) 0,6 и 4/7
1) т.к. дробь 4/7 не перевести в десятичную, переведём десятичную дробь 0,6 в обыкновенную:
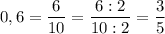
2) приведём дроби к НОЗ:
5 и 7 - простые числа
НОК (5; 7) = 5 * 7 = 35
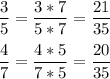
3) сравним дроби:
правило: из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше
Т.к. 21 > 20, значит:
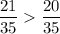 т.е.
т.е. 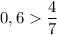
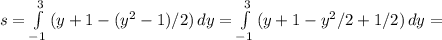
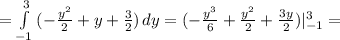
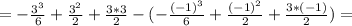
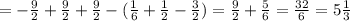 ед².
ед². 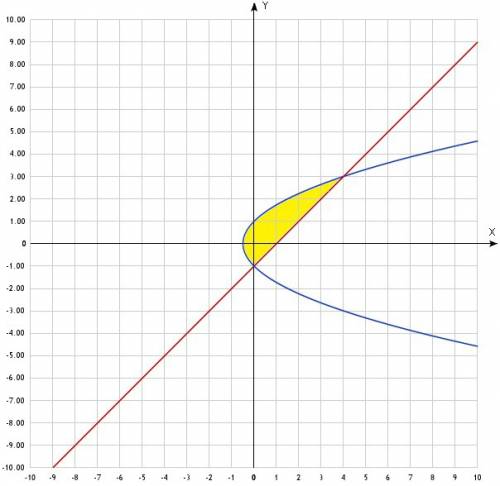
значит больший острый угол=60°